Speaker
Description
Introduction
We present an analytical Bloch simulation approach for arbitrary MRI sequence simulation called Phase Distribution Graphs. It is a general implementation of the Extended Phase Graph (EPG) concept, based on the Fourier-domain Bloch equation, but with arbitrary timing, and including the exact contribution of dephased states resulting from spatial encoding and T2’ relaxation effects. In contrast to EPG, which was limited to echo amplitudes only, this allows calculation of full echo shapes. Our Pytorch implementation provides full differentiability in all input parameters allowing gradient descent optimization. A major problem of phase graphs, the generation of an „astronomical number of states“ is solved by an efficient state selection algorithm. The simulation compares well to results of conventional Bloch simulations with quasi-random isochromat distribution, which it outperformed in simulation time by at least one order of magnitude. Different sequences and their artifacts are analyzed and improved, underlining that Phase Distribution Graphs allow efficient simulation and optimization of arbitrary MRI sequences, which was previously only possible via high isochromat counts.
Theory
In contrast to EPG \footnote{Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes - pure and simple. J Magn Reson Imaging. 2015 Feb;41(2):266-95. doi: 10.1002/jmri.24619.}, which describes magnetization states as plane waves $e^{i\mathbf{k}\cdot\mathbf{r}} $, we propose to modify the magnetization to be represented by a more complex state, but still a single state $ F^ {\hat{e} }_{k,\tau} $:
$M^ {\hat{e}}(\mathbf{r},\omega) = F^ {\hat{e}}_{k,\tau} \cdot e^{i\mathbf{k}\cdot\mathbf{r}} \cdot e^{i\tau\omega} \cdot W(\omega,\mathbf{r}) \cdot V(\mathbf{r}) $
Including the spatial distribution V (voxel positions and shape) and the spectral distribution W (T2‘ dephasing).
Assuming a sinc voxel shape for V, and a Cauchy-Distribution ($\Delta\omega_0$, T2‘) for W the full simulated measurable MRI signal is given by the sum of all + states, integrated over space $\mathbf{r}$ and all frequencies $\omega$ leading to
$S = \sum_{\nu} \sum_{k,\tau} F^ {+}_{k,\tau} \cdot (e^{i\Delta\omega_0\tau} \cdot e^{-|\tau|/T'_2}) \cdot \left( e^{i\mathbf{k} \cdot \mathbf{r}_{{\nu} } } \cdot \Theta \left(\mathbf{k}-\mathbf{k}_{{\nu} } \right) \right) $
, i.e., the sum over all $k$-and $\tau$-dephased +-states of all voxels $\nu$. Here $\Theta$ is the Heaviside function limiting k to the first k-space.
A single pre-pass calculation of this signal equation allows us to identify the most important states of a certain MRI sequence, and we can define by a threshold the trade-off between duration and accuracy of the simulation.
Results
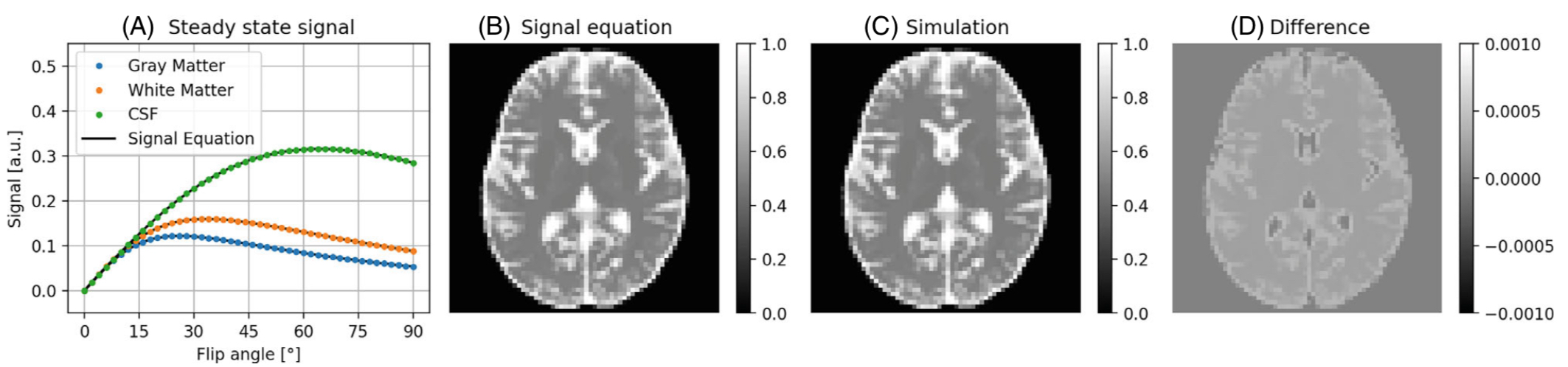
Figure 1 shows the match between our simulation and the analytical solution of a bSSFP sequence. Figure 2 shows comparison to an isochromat solution in the case of 90 degree SSFP with a large fraction of dephased magnetization. The run time analysis shows that PDG outperforms conventional Bloch simulations in such cases by two orders of magnitude.
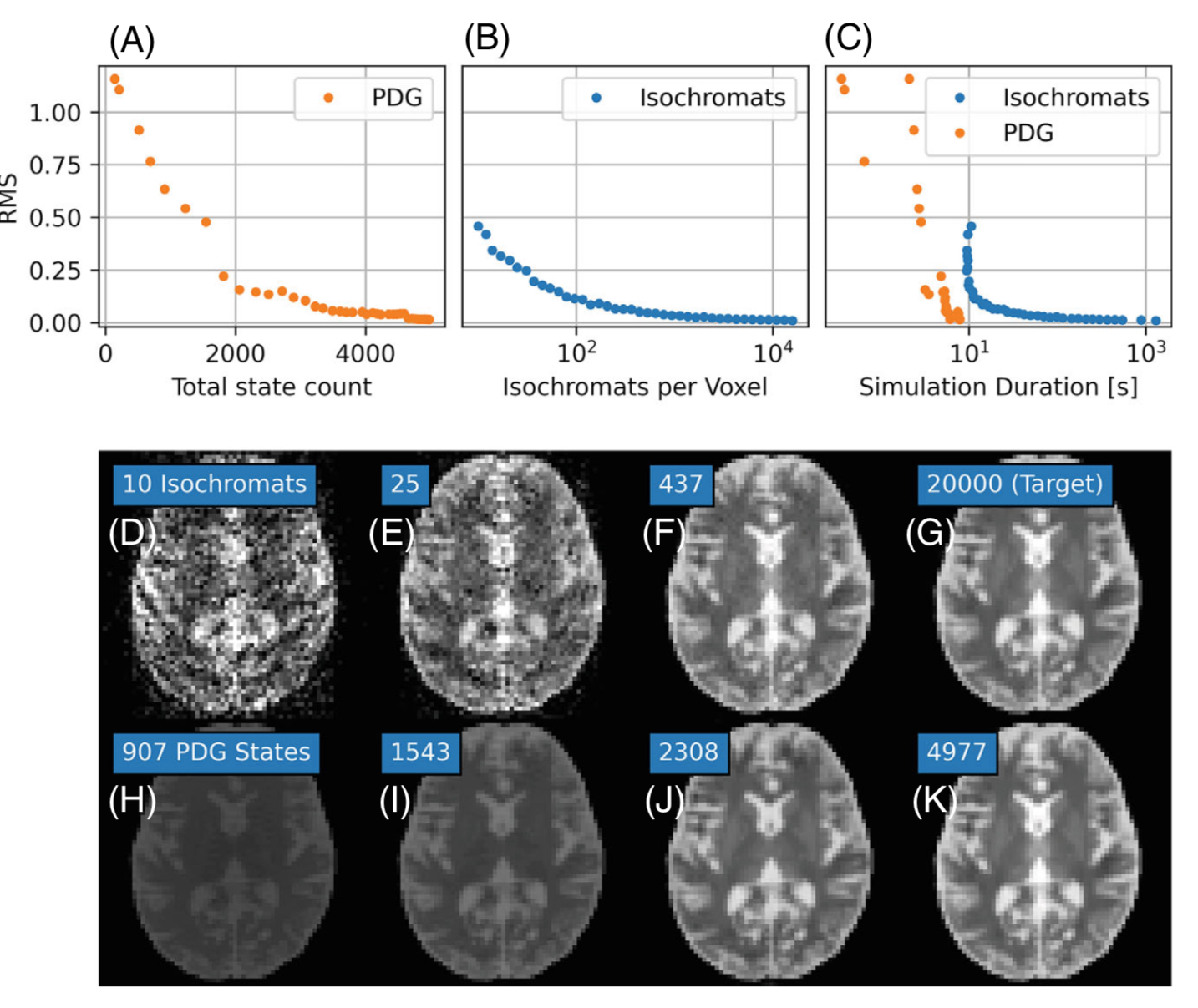
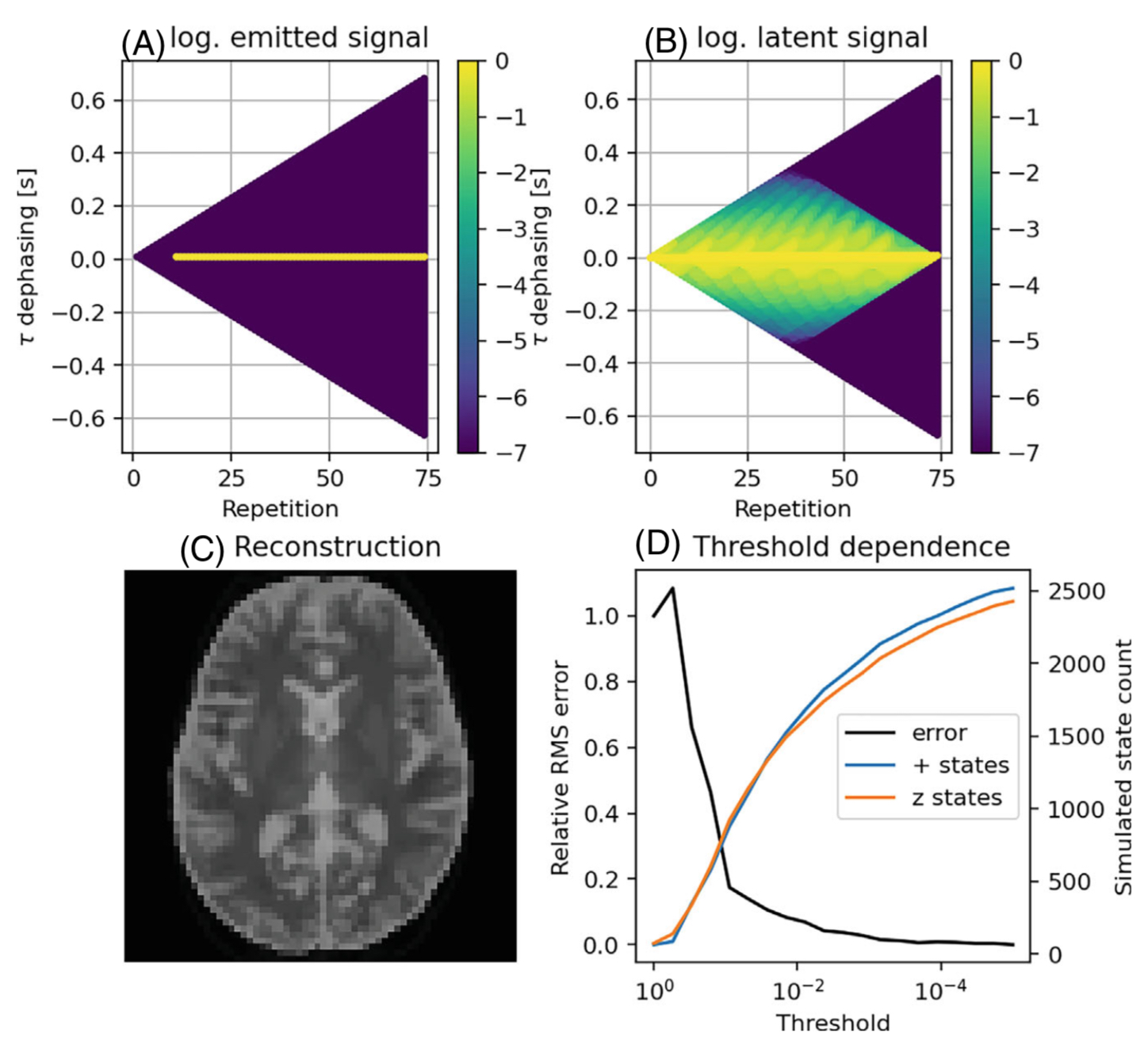
Figure 3 shows the phase graph plot of the emitted signal and the newly introduced latent signal. The latter is used to select the important states of the sequence. Stronger relaxation or diffusion actually reduces the number of necessary states for a given accuracy.
With this approach we optimized several MRI sequences (data not shown) with regard to artifacts (FLASH), blurring (TSE) and homogeneity (pTx-TSE).
Discussion and Conclusion
In this work, we derived and implemented a fully differentiable Bloch simulation based on the principles of EPG. Contrary to current EPG simulations, it is capable of simulating the actual MRI signal of arbitrary sequences, while exhibiting the same advantages like efficient computation and no simulation noise. This makes it possible to simulate and optimize sequences that otherwise would need a vast number of isochromats to be described correctly, making it a suitable replacement for these applications. Furthermore, additional analysis of magnetization and signal is possible that is not available with other simulation techniques.
The differentiable implementation allows gradient descent optimization of all parameters.
Open Science
All codes are documented and available open source via
https://mrzero-core.readthedocs.io/
