IFIP TC7 System Modeling and Optimization

Aug 12, 2024, 9:00 AM → Aug 16, 2024, 2:50 PM Europe/Berlin

Von-Melle-Park 8

General information

The complexity of the problems crucial for understanding the technical, social and, more broadly, systemic challenges related to today's reality, requires the creation and application of appropriate mathematical models and their optimization. Today's world is flooded with an unimaginable amount of data, the usefulness of which depends on the way they are incorporated into mathematical models, which make it possible to explain the nature of the processes and, what is particularly important, to forecast of the future.

The credibility of forecasts is critical for systemic decision-making support, often of a strategic aspect. Without a proven methodology for constructing mathematical models and optimizing them for specific types of applications, it would not be possible to ensure the quality of decisions based on them.

The environmental and climate crisis generate a great class of challenges in this matter, covering the problems of sustainable socio-economic development at all levels, from individual to global. Increasing violent weather phenomena, insufficient efficiency of energy systems, and recently a new scale of epidemic challenges are spectacular examples showing the role of effective management, down to the level of optimal control in close to real time.

IFIP (International Federation of Information Processing) TC-7 (Technical Committee - 7) "System Modeling and Optimization" conferences, grouping the world's most outstanding specialists in this field, have been held for over 50 years. The 31st conference "System Modeling and Optimization" will be held in Hamburg on August 12-16, 2024 (tentative date).

The scope of TC7 consists in computational aspects of optimization problems arising in such areas as Aerospace, Biomedicine, Economics, Meteorology, and Public Services (Health, Environment, Police, Fire, Transportation, etc.). Some specific examples are:

• on-line and off-line computational techniques in modeling and control of dynamic systems;
• trajectory analysis and computation;
• optimization of decentralized systems (macro-economic systems) and systems with multicriteria;
• optimization of resource allocation in urban systems;
• optimization of pollution-control systems;
• optimization of man-machine systems;
• optimization of power systems operation;
• risk management in particular in mathematical finance and insurance;
• development of machine learning techniques;
• optimization and control under uncertainty;
• Optimal Control of Systems Governed by Differential (Ordinary and Partial) Equations;
• Hybrid, Algebraic-Differnetial Equations;
• Modeling and Simulation of Distributed Parameter Systems;
• Inverse Problems;
• Nonlinear, Discrete, and Stochastic Optimization;
• Computational Optimization;

short-programm & dinner directions

Monday, August 12

9:00 AM → 10:00 AM Registration

10:00 AM → 10:30 AM Opening/Closing: Opening

10:30 AM → 12:30 PM Plenary Talk

10:30 AM Optimization Problems with probabilistic/robust (probust) constraints: Theory, Numerics and Applications

Probabilistic Constraints have become one of the most popular tools to deal with uncertain inequality constraints in engineering problems. When a decision has to be taken prior to observing uncertain parameters affecting the constraint, then it is very natural to define a decision as feasible whenever the uncertain constraint is satisfied with high probabilty. Due to the absence of explicit formulae, such inequalities introduce a lot of challenges in their analysis and algorithmic treatment. This is the more true if the random inequality system is not finite but infinite. Then, the index of the system can be interpreted as another uncertain parameter of 'robust' (non-stochastic) nature. This gave rise to i troduce the class of so-called probabilistic/robust, shortly: probust constraints. The talk addresses analytical properties, such as semi-continuity, Lipschitz continuity, differentiability, existence of solutions and optimality conditions for probust constraints. Moreover, numerical approaches via the so-called spherical-radial decomposition and adaptive index refinement are presented and some applications in energy management (capacity maximization in gas networks, water reservoir management) are discussed.

Speaker: Prof. René Henrion (Weierstrass Institute for Applied Analysis and Stochastics)

11:30 AM Generative Modeling via Wasserstein Gradient flows of Maximum Mean Discrepancies

This talk is concerned with inverse problems in imaging from
a Bayesian point of view, i.e. we want to sample from the posterior distribution given noisy measurement. We tackle the problem by studying gradient flows of particles in high dimensions. More precisely, we analyze Wasserstein gradient flows of maximum mean discrepancies defined with respect to different kernels,
including non-smooth ones. In high dimensions, we propose the efficient flow computation via Radon transform (slicing) and
subsequent sorting or random Fourier features. Special attention is paid to non-smooth Riesz kernels. We will see that Wasserstein gradient flows of corresponding maximum mean discrepancies have a rich structure. In particular, singular measures can become absolutely continuous ones and conversely.
Finally, we approximate our particle flows by conditional generative neural networks and apply them for conditional image generation and in inverse image restoration problems like computerized tomography and superresolution.

This is joint work with
J. Hertrich (UCL) and
P. Hagemann, F. Altekrüger, R. Beinert,
J. Chemseddine, M. Gräf, Ch. Wald (TU Berlin).

References:
P. Hagemann, J. Hertrich, F. Altekrüger, R. Beinert, J. Chemseddine and G. Steidl.
Posterior sampling based on gradient flows of the MMD with negative distance kernel.
ICLR 2024.

J. Hertrich, M. Gräf, R. Beinert and G. Steidl.
Wasserstein steepest descent flows of discrepancies with Riesz kernels.
Journal of Mathematical Analysis and Applications 2024.

F Altekrüger, P. Hagemann and G. Steidl.
Conditional generative models are provably robust: Pointwise guarantees for Bayesian inverse problems.
Transactions on Machine Learning Research 2024

F. Altekrüger, J. Hertrich and G. Steidl.
Neural Wasserstein Gradient Flows for Maximum Mean Discrepancies with Riesz Kernels.
ICML 2023

Speaker: Prof. Gabriele Steidl (TU Berlin)

12:30 PM → 2:00 PM Lunch

2:00 PM → 3:30 PM MS 01: Optimal Control and Machine Learning: MS 01-1

2:00 PM Data-driven predictive control with stability guarantees

Extended Dynamic Mode Decomposition is a popular data-driven method to approximate the flow of a dynamical control system through the lens of observable functions. In this talk, we discuss how this framework and corresponding finite-data error bounds may be used in data-driven Model Predictive Control to establish (practical) asymptotic stability. The key ingredient are proportional error bounds vanishing at the origin, which may be utilized to show that important system-theoretic properties, such as cost controllability, carry over to the data-driven model, if a sufficient amount of samples is chosen.

Speaker: Manuel Schaller

2:30 PM A relaxation-based probabilistic approach for PDE-constrained optimization under uncertainty with pointwise state constraints

We consider a class of convex risk-neutral PDE-constrained optimization problems subject to pointwise control and state constraints. Due to the many challenges asso- ciated with almost sure constraints on pointwise evaluations of the state, we suggest a relaxation via a smooth functional bound with similar properties to well-known probability constraints. First, we introduce and analyze the relaxed problem, discuss its asymptotic properties, and derive formulae for the gradient the adjoint calculus. We then build on the theoretical results by extending a recently published online con- vex optimization algorithm (OSA) to the infinite-dimensional setting. Similar to the regret-based analysis of time-varying stochastic optimization problems, we enhance the method further by allowing for periodic restarts at pre-defined epochs. Not only does this allow for larger step sizes, it also proves to be an essential factor in obtain- ing high-quality solutions in practice. The behavior of the algorithm is demonstrated in a numerical example involving a linear advection–diffusion equation with random inputs. In order to judge the quality of the solution, the results are compared to those arising from a sample average approximation (SAA). This is done first by comparing the resulting cumulative distributions of the objectives at the optimal solution as a function of step numbers and epoch lengths. In addition, we conduct statistical tests to further analyze the behavior of the online algorithm and the quality of its solutions.

Speaker: Mathias Staudigl

3:00 PM A Greedy Algorithm for Efficient Learning of Control Systems

The efficiency of training data is a prominent issue in machine learning. While too little data can lead to insufficient learning, too much data can result in overfitting or can be computationally expensive to generate.
In this talk, we investigate a class of greedy-type algorithms that have previously proven to compute efficient control functions for the reconstruction of operators in dynamical systems. We introduce an adapted version of these algorithms to learn the control-to-state map of a dynamical system by the means of a neural network.
The main goal of this strategy is to make the trained network robust with respect to the input control functions, while using the least amount of training data. We demonstrate the efficiency of this method by numerical experiments.

Speaker: Simon Buchwald

2:00 PM → 3:30 PM MS 04: Correlation-based passive imaging and optimal experimental design: MS 04-1

2:00 PM Correlation imaging in telescope imaging and beyond

In this talk I discuss correlation imaging in the context of adaptive optics in next generation telescope imaging. Moreover, I discuss the connections to covariance estimation in statistics.

Speaker: Tapio Helin (LUT University)

2:30 PM Inferring solar differential rotation and viscosity via passive imaging with inertial waves

The recent discovery of inertial waves on the surface of the Sun offers new possibilities to learn about the solar interior. These waves are long-lived with a period on the order of the Sun rotation period (~27 days) and are sensitive to parameters deep inside the Sun. They are excited by turbulent convection, leading to a passive imaging problem. In this work, we present the forward and inverse problem of reconstructing viscosity and differential rotation on the Sun from cross-covariance observations of these inertial waves.

Speaker: Tram Nguyen (Max Planck Institute for Solar System Research)

2:00 PM → 3:30 PM MS 05: Parallel-in-time methods for PDE-constrained optimization: MS 05-1

2:00 PM Parallelization in time for optimal control and inverse problems

Algorithms for the numerical solution of optimization problems with time-dependent PDEs are computationally extremely demanding, as they require multiple PDE solves during the iterative optimization process. With today's modern computers, the time-to-solution can be decreased through massive parallelization, which is traditionally done in the spatial dimensions, but more recently also in the time domain. In this talk, we discuss approaches to use parallel-in-time methods for the solution of PDE-constrained optimization problems, and present numerical examples.

Speaker: Dr Sebastian Götschel (TU Hamburg)

2:30 PM Time Parallel KKT Preconditioners for Transient PDE-Constrained Optimization

Many physics-informed data integrated modeling approaches require the solution of optimization problems with evolutionary constraints. This talk develops scalable algorithms for transient PDE-constrained optimization. Here, simulation-based optimization repeatedly executes the simulator’s forward and adjoint time integration schemes. Consequently, the arrow of time creates a sequential bottleneck in the optimization algorithm. Further, for performance these methods rely strongly on spatial parallelization for the forward and adjoint solves. Thus, when forward and adjoint solvers are already operating at the limit of strong scaling, the arrow-of-time bottleneck cannot be mitigated by adding additional computing resources.

To address this bottleneck we have developed approaches to parallelize over the time domain, alleviating the serialization burden and yielding faster optimization. We propose a domain decomposition and multigrid preconditioner for solving the KKT system arising in sequential quadratic programming. These approaches leverage the observation that the Schur-complement is elliptic in time, and thus our approaches our based on domain decomposition and multigrid techniques. The performance of these preconditioners is examined in an empirical study demonstrating the approach is scalable with respect to the number of time steps and subdomains.

Speaker: Eric C. Cyr (Sandia National Laboratories)

3:00 PM Parallel-in-time multiple shooting for large-scale optimal control problems governed by the 3D Navier-Stokes equations

In recent years, multiple shooting methods have found their way from simple ODE-based optimization to tackling more intricate, moderate to large-scale PDE-based problems. By fully exploiting the multiple shooting paradigm through parallel-in-time integration of the shooting windows, it may allow for substantial parallel speed-ups, thereby accelerating the convergence of the optimization. This study applies the multiple shooting algorithm to optimal control problems governed by the three-dimensional Navier-Stokes equations. An augmented Lagrangian penalty method is used to solve the equality-constrained optimization problem arising from the multiple shooting formulation. To deal with the large-scale nature of the PDE-based problem, we employ limited-memory BFGS to solve the unconstrained subproblem in each augmented Lagrangian outer iteration. The gradient computation relies on a temporally-discrete adjoint method, where the forward and adjoint PDE evaluations are efficiently parallelized, both in space (through 3D domain decomposition) and time (through parallel-in-time integration over the shooting window).
The algorithm is validated on large-scale, tracking-type optimization problems featuring up to $10^8$ design variables and employing up to $100$ windows in the multiple shooting framework. Given the embarrassingly parallel nature of the parallel-in-time integration intrinsic to the multiple shooting approach, our framework enables significant parallel(-in-time) speed-ups. It is also shown that the convergence of the method and the resulting algorithmic speed-ups heavily depend on the initialization of the shooting windows. Nonetheless, for the optimization problems considered here, the initialization follows naturally from the tracking-type formulation and even enables algorithmic speed-ups up (independent of the parallel-in-time techniques). Finally, we demonstrate how the multiple shooting method significantly outperforms single shooting (when the number of windows is high enough), and that the proposed parallel-in-time framework surpasses spatial parallelization alone (especially when the latter is saturated), allowing for an optimal allocation of computational resources.

Speaker: Nick Janssens (KU Leuven)

2:00 PM → 3:00 PM MS 10: Inverse Problems for Partial Differential Equations: MS 10-1

2:00 PM Optimal control of the principal coefficient in a scalar wave equation

We consider optimal control of the scalar wave equation where the control enters as a coefficient in the principal part. Adding a total variation penalty allows showing existence of optimal controls, which requires continuity results for the coefficient-to-solution mapping for discontinuous coefficients. We additionally consider a so-called multi-bang penalty that promotes controls taking on values pointwise almost everywhere from a specified discrete set. Under additional assumptions on the data, we derive an improved regularity result for the state, leading to optimality conditions that can be interpreted in an appropriate pointwise fashion. The numerical solution makes use of a stabilized finite element method and a nonlinear primal-dual proximal splitting algorithm.

Speaker: Christian Clason (University of Graz)

2:30 PM Conditional gradient methods in total variation regularization of inverse problems for PDEs

A very common ansatz in inverse problems for PDEs is that the sought solutions are piecewise constant, modelling situations like localized inclusions of different material properties within an otherwise homogeneous medium. In this situation, variational regularization with a total variation penalty balances being compatible with piecewise constant minimizers with retaining convexity of the regularizer. However, its lack of differentiability means that most numerical methods require some level of smoothing, so that such piecewise constant structures can be observed only approximately and/or at very fine resolutions.

In this work, we instead consider generalized conditional gradient methods that provably approximate minimizers as linear combinations of characteristic functions, by alternating insertion and correction steps. Specifically, we focus on a discretised setting of functions defined on triangulations. This framework allows standard FEM discretizations to coexist with fast graph cut approaches to the total variation, which have long been used in image segmentation and related tasks. We present variants of such methods which allow for pointwise constraints and insertion steps with as small as possible computational cost. After considering some convergence results, these are applied in various canonical test cases, such as inverse source problems with different kinds of measurements.

Speaker: Jose A. Iglesias (University of Twente)

3:30 PM → 4:00 PM Coffee Break

4:00 PM → 5:00 PM MS 01: Optimal Control and Machine Learning: MS 01-2

4:00 PM On the convergence of feedback laws generated via machine learning methods

The synthesis of feedback laws for infinite horizon via machine learning methods instead of classical methods has been a theme of interest in recent years, since they have the potential of mitigate the curse of dimensionality. There are two methods which are under study in this talk.

The first consists in looking for a feedback law in a finite dimensional functional space (for example polynomials, neural networks, RKHS) which minimize the averaged cost functional of the control problem with respect to a set of initial conditions. The second one corresponds to a regression method which minimizes the $L^2$ distance in the space of the controls. For the first method we provide a convergence result which relies on the existence of a sequence of smooth approximating optimal feedback laws. Further, the existence of such a sequence is proved relying on the Hölder continuity of the value function and the existence of a Lyapunov type function.

On the other hand, for the regression method we are able to prove the convergence by assuming that the value function is smooth. Additionally, we present a family of infinite horizon optimal control problem for which the degree of smoothness of the value function depends on a penalty parameter. This dependence is such that the value function is $C^2$ when the penalty parameter is close to 0 and is non-smooth but Lipschitz when it is large. Through this problem we are able to compare the behavior of the methods depending on the degree of smoothness of the value function by performing numerical realizations for both approaches.

Speaker: Donato Vásquez Varas (Johann Radon Institute for Computational and Applied Mathematics (RICAM))

4:30 PM Adaptive Step Sizes for Preconditioned Stochastic Gradient Descent

The choice of the step size (or learning rate) in stochastic optimization algorithms, such as stochastic gradient descent, plays a central role in the training of machine learning models. Both theoretical investigations and empirical analyses emphasize that an optimal step size not only requires taking into account the nonlinearity of the underlying problem, but also relies on accounting for the local variance within the search directions. In this presentation, we introduce a novel method capable of estimating these fundamental quantities and subsequently using these estimates to derive an adaptive step size for stochastic gradient descent. Our proposed approach leads to a nearly hyperparameter-free variant of stochastic gradient descent. We provide theoretical convergence analyses in the special case of stochastic quadratic, strongly convex problems. In addition, we perform numerical experiments focusing on classical image classification tasks. Remarkably, our algorithm exhibits truly problem-adaptive behavior when applied to these problems that exceed theoretical boundaries. Moreover, our framework facilitates the potential incorporation of a preconditioner, thereby enabling the implementation of adaptive step sizes for stochastic second-order optimization methods.

Speaker: Frederik Köhne (Universität Bayreuth)

4:00 PM → 5:30 PM MS 04: Correlation-based passive imaging and optimal experimental design: MS 04-2

4:00 PM Optimal experimental design with correlation data

A major problem within the field of aeroacoustics is determining the distribution of an aeroacoustic source, such as an airplane engine, given pressure measurements on external microphone arrays. Taking a Bayesian view and modeling the source as fundamentally random with zero mean leads to the problem of determining the covariance of the random source.

While this can be recovered from correlations of pressure measurements, the consequent dimensionality increase is significant when the dimension of the observations is large. Accordingly, we study optimal experimental design for correlation data, with the goal of determining the optimal, sparse sensor placement prior to conducting any real-world experiments.

Specifically, we investigate A-optimal designs, that is, designs that minimize the average posterior covariance in the reconstruction. Building on the work presented in [1] for the case of deterministic sources with non-correlated data, we moreover present algorithmic treatment of the design problem for the random source problem in aeroacoustics and other PDE-based applications, involving low-rank approximation of correlated forward operators.

[1] A. Alexanderian, Optimal experimental design for infinite-dimensional Bayesian inverse problems governed by PDEs: a review, Inverse Problems, 37(2021), 043001.

Speaker: Christian Aarset (University of Göttingen)

4:30 PM Scalable Method for Bayesian Experimental Design Using the Projection-Based Approximation of Conditional Expectation (PACE)

We address the computational efficiency of the A-optimal Bayesian design of experiments . A-optimality is a widely used criterion in Bayesian experiment design, aiming to minimize the expected conditional variance and find the optimal design. We propose a novel likelihood-free method for the A-optimal experiment design that does not require sampling or approximating the Bayesian posterior distribution, avoiding issues with posterior intractability. Our approach leverages two principle properties of the conditional expectation: the law of total variance and the orthogonal projection property. By utilizing the law of total variance, we obtain the expected conditional variance through the variance of the conditional expectation. Furthermore, we exploit the orthogonal projection property to approximate the conditional expectation using regression, eliminating the need for likelihood function evaluation. To implement our approach, we employ deep artificial neural networks (ANN) for approximating the nonlinear conditional expectation. Particularly for continuous experimental design parameters, we integrate the minimization of the expected conditional variance into the training process of the ANN-based approximation. This integration is enabled by the shared objective function, leading to improved algorithm efficiency. Through numerical experiments, we demonstrate that our method significantly reduces the number of computationally expensive forward-model evaluations compared to common likelihood-based approaches, effectively overcoming a significant bottleneck.

Speaker: Vinh Hoang (RWTH Aachen University)

5:00 PM Approximative optimal experimental design in Bayesian inversion

Many inverse problems in science and engineering are often subject to uncertainty, especially when the measurement data is complex and indirect. To reduce uncertainty, one needs to find a way to measure the data efficiently. This problem falls under the umbrella of the optimal experimental design (OED). The computational cost of OED, however, is notoriously expensive, so in practice, one inevitably has to work with surrogate models, approximations and alike.

While the approximation problem in Bayesian inverse problems (BIPs) has been studied intensively in the last decade ([3]), their counterparts in OED have only been considered recently. In recent works, we proposed a general framework to study the stability properties of the expected utility function for the optimal experimental design in BIPs. We investigate this problem in a non-parametric setting and provide convergence rates of the expected utility with respect to likelihood perturbations as well as prior perturbations. This talk is based on [1, 2].

\textbf{References}\
[1] D.-L. Duong, T. Helin and J.R. Rojo-Garcia, Stability estimates for the expected utility in Bayesian optimal experimental design, \textit{Inverse Problems}, Vol. \textbf{39(12)}, 125008, 2023.\
[2] D.-L. Duong \emph{et al.}, Stability for the Bayesian optimal experimental design under prior perturbations, upcoming, 2024+.\
[3] A.M. Stuart, Inverse problems: a Bayesian perspective, \textit{Acta numerica}, Vol. \textbf{19}, pp. 451-559, 2010.{Acta numerica}, Vol. \textbf{19}, pp. 451-559, 2010.

Speaker: Duc-Lam Duong (LUT University)

4:00 PM → 5:30 PM MS 05: Parallel-in-time methods for PDE-constrained optimization: MS 05-2

4:00 PM A Periodic-in-Time Approximation for Parallel Preconditioning of Instationary Stokes and Oseen Problems

PDE-constrained optimization problems arise in various applications in industry and can also be useful in other mathematical fields. Applications can be found in physics, chemistry, biology, medical imaging, optimal transport, and many other areas. Due to the lack of analytical solutions to these problems in general, the fast and robust numerical solution is of utmost importance. However, the discretization of such problems often results in huge-scale systems of linear or possibly also non-linear equations. Black-box solvers, such as direct solvers for linear systems, often fail when applied to these systems.
During recent years, preconditioned iterative methods have been successfully applied to a range of PDE-constrained optimization problems, including large-scale flow control problems, on which we focus here.

In this talk, we will explore a diagonalization-based approach to create effective preconditioners for a range of problems, including unsteady Stokes and Oseen control. Our methodology involves approximating the original problem by a time-periodic equivalent, allowing us to perform a temporal diagonalization. This results in a parallel-in-time preconditioner tailored for solving complex flow control problems. Our approach demonstrates robustness with respect to model parameters and the discretization, and its efficiency is verified in numerical experiments.

Speaker: Bernhard Heinzelreiter (University of Edinburgh)

4:30 PM A New Diagonalization Based Method for Parallel-in-Time Solution of Linear-Quadratic Optimal Control Problems

This talk will introduce a new diagonalization technique for the parallel-in-time solution of linear-quadratic optimal control problems with time-invariant system matrices. The target problems are often derived from a semi-discretization of a Partial Differential Equation (PDE)-constrained optimization problem. The solution of large-scale time dependent optimal control problems is computationally challenging as the states, controls, and adjoints are coupled to each other throughout the whole time domain. This computational difficulty motivates the use of parallel-in-time methods. For time-periodic problems the diagonalization efficiently transforms the discretized optimality system into $n_t$ (=number of time steps) decoupled complex valued $2n_y \times 2n_y$ systems, where $n_y$ is the dimension of the state space. These systems resemble optimality systems corresponding to a steady-state version of the optimal control problem and they can be solved in parallel across the time steps, but are complex valued. For optimal control problems with initial value state equations a direct solution via diagonalization is not possible, but an efficient preconditioner can be constructed from the corresponding time periodic optimal control problem. The preconditioner can be efficiently applied parallel-in-time using the diagonalization technique. In addition, this diagonalization technique combined with a tailored ADMM algorithm yields a parallel-in-time solution to linear-quadratic optimal control problems with inequality constraints on the state and/or control.

Speaker: Nathaniel Kroeger (Rice University)

5:00 PM Parallel-in-Time Bathymetry Reconstruction

For the prediction and study of water flows in a river or channel the knowledge of the bottom topography - the bathymetry - is required. Direct measurements of bathymetries are possible, but can be very expensive and time consuming. This motivates the development of methods to reconstruct a bathymetry numerically. In this talk, an approach will be shown that uses measurements of the water surface for the reconstruction. By defining an optimisation problem that is constrained by the one-dimensional shallow water equations it is possible to obtain an approximation on the real bathymetry. In this context, we investigate the use of Parallel-in-time methods in order to accelerate the computations.

Speaker: Judith Angel

4:00 PM → 5:30 PM MS 10: Inverse Problems for Partial Differential Equations: MS 10-2

4:00 PM Identification of cavities in a nonlinear model arising from electrophysiology

Detecting ischemic regions is paramount in preventing potentially fatal ventricular ischemic tachycardia. Traditionally, this involves capturing the heart's electrical activity through noninvasive or minimally invasive methods, such as body surface or intracardiac measurements. Insight into utilizing electrical measurements for ischemia detection can be gained through mathematical and numerical models of cardiac electrophysiology.
The ultimate objective is to integrate boundary measurements of potentials with a mathematical model of the heart's electrical activity to pinpoint the location, shape, and size of ischemic regions and/or infarctions.
A promising approach involves modeling ischemic regions as electrical insulators using the monodomain model.
This model, a semilinear reaction-diffusion system, provides a comprehensive description of cardiac electrical activity.
I will show that perfectly insulating regions can be uniquely determined by partial boundary measurements of the potential.

Speaker: Andrea Aspri (University of Milan)

4:30 PM Monotonicity and Convexity in Inverse Coefficient Problems

Several applications in medical imaging and non-destructive material testing lead to inverse elliptic coefficient problems, where an unknown coefficient function in an elliptic PDE is to be determined from partial knowledge of its solutions. This is usually a highly non-linear ill-posed inverse problem, for which unique reconstructability results, stability and resolution estimates and global convergence of numerical methods are very hard to achieve. In this talk we will review some recent results on Loewner Monotonicity and Convexity that may help in overcoming these issues.

Speaker: Bastian Harrach (Goethe University Frankfurt, Germany)

5:30 PM → 8:30 PM Welcome Reception

Tuesday, August 13

9:00 AM → 10:30 AM MS 01: Optimal Control and Machine Learning: MS 01-3

9:00 AM Approximating optimal value functions with neural networks under a decaying sensitivity assumption

In this presentation, we consider interconnected optimal control problems, wherein the interconnection is represented as a graph. We establish a decaying sensitivity condition, where the influence between graph nodes diminishes with their distance, and leverage this assumption to construct a separable approximation of the optimal value function. This approach allows us to identify scenarios in which neural networks can effectively address the curse of dimensionality associated with approximating optimal value functions, requiring only polynomial growth in the state dimension for the number of neurons. Additionally, we outline a suitable neural network architecture and corresponding training algorithm. To provide empirical validation of our theoretical framework, we present results from a numerical test case.

Speaker: Mario Sperl (University of Bayreuth)

9:30 AM A Recursive Multilevel Algorithm for Deep Learning

As the use cases for neural networks become increasingly complex, modern neural networks must also become deeper and more intricate to keep up, indicating the need for more efficient learning algorithms. Multilevel methods, traditionally used to solve differential equations using a hierarchy of discretizations, offer the potential to reduce computational effort.

In this talk, we combine both concepts and introduce a multilevel stochastic gradient descent algorithm that accelerates learning through a multilevel strategy. A gradient correction term is needed to establish first-order consistency.
We discuss convergence of the method in the case of a deterministic gradient correction as well as a stochastic gradient correction under additional conditions including step size regularization and an angle condition.

To demonstrate the usefulness of our approach, we apply it to residual neural networks in image classification. The resolution of the images is utilized to generate data sets of varying complexity, which are then used to build a hierarchy of neural networks with a decreasing number of variables. Additionally, we construct corresponding prolongation and restriction operators. Numerical results are presented.

Speaker: Isabel Jacob (TU Darmstadt)

10:00 AM Dissipativity Properties in Neural Network Training

System-theoretic dissipativity notions introduced by Jan C. Willems play a fundamental role in the analysis of optimal control problems. They enable the understanding of infinite-horizon asymptotics and turnpike properties. This talk introduces a dissipative formulation for training deep Residual Neural Networks (ResNets) in classification problems. To this end, we formulate the training of ResNets with a constant width as an optimal control problem and investigate its dissipativity properties when introducing a stage cost based on a variant of the cross entropy loss function, the classic loss function for classification tasks.

We illustrate the dissipative formulation by training on the MNIST dataset, which exhibits the turnpike phenomenon: the data remains unchanged throughout several layers. These layers can then be removed without changing the transformation learned by the NN. This technique can be used to obtain shallow neural networks for a given classification task with simplified hyperparameter tuning.

Speaker: Jens Püttschneider (TU Dortmund)

9:00 AM → 10:30 AM MS 04: Correlation-based passive imaging and optimal experimental design: MS 04-3

9:00 AM Bayesian Inversion for Semiconductor Inverse Problems

Semiconductor devices such as nano-biosensors have many applications in our real life including medical applications for diagnostic purposes. In this work, we describe incorporating uncertainties in the mathematical modeling of semiconductor devices, as well as the propagation of uncertainties in the solution of the corresponding PDE model. We then formulate and solve a Bayesian inverse problem for the nanoscale devices. To this end, we first show that the parameter-to-observable map corresponding to this inverse problem satisfies sufficient conditions to guarantee the well-posedness properties of the proposed Bayesian inversion approach. Then, we propose a Markov-chain Monte-Carlo method for the Bayesian posterior estimation of the unknown parameters from the voltage-current measurements.

Speaker: Leila Taghizadeh (TU Wien)

9:30 AM Optimality of Pulse Energy for Photoacoustic Tomography

Photoacoustic tomography (PAT) is a rapidly evolving imaging technique that combines the high contrast of optical imaging with the high resolution of ultrasound imaging. When dealing with typically noisy measurement data, one aims to identify certain parameters in the governing PDEs for the photoacoustic tomography system. Therefore, an essential factor in estimating these parameters is the system's design, which typically involves multiple factors that can affect the accuracy of reconstruction. In this work, we employ a Bayesian approach to solving a PAT inverse problem with the goal of optimizing the laser pulse of the PAT system to minimize the uncertainty in the reconstructed parameters. Additionally, we account for wave propagation attenuation in the inverse problem of PAT, which is governed by a fractionally damped wave equation. Finally, we illustrate the effectiveness of our proposed method using a numerical simulation.

Speaker: Phuoc Truong Huynh

10:00 AM Experimental design in the presence of model error

In inverse problems, one often assumes a model for how the data is generated from the underlying parameter of interest. In experimental design, the goal is to choose observations to reduce uncertainty in the parameter. When the true model is unknown or expensive, an approximate model is used that has nonzero `model error' with respect to the true data-generating model. Model error can lead to biased parameter estimates. If the bias is large, uncertainty reduction around the estimate is undesirable. This raises the need for experimental design that takes model error into account. We present a framework for model error-aware experimental design in Bayesian inverse problems. Our framework is based on Lipschitz stability results for the posterior with respect to model perturbations. We use our framework to show how one can combine experimental design with models of the model error in order to improve the results of inference.

Speaker: Nada Cvetkovic

9:00 AM → 10:30 AM MS 09: Stochastic Modeling and Control: MS 09-1

9:00 AM On the value of a time-inconsistent mean-field optimal stopping"

I will review some recent results on optimal stopping and zero-sum Dynkin games problems for time-inconsistent models including recursive utility functions of mean-field type.

Speaker: Boualem Djehiche (KTH Royal Institute of Technology)

9:30 AM Bellman equation for risk-sensitive control with superlinear cost

We consider the finite horizon risk-sensitive control problem for a system driven by a standard Brownian motion. We control the system only through the drift, the control set is unbounded, and the cost/reward function is superlinear with respect to the control variable. To solve the problem, we use the HJB theory and prove that the associated PDE admits a classical ($C^{2,1}$) solution.

Speaker: Dariusz Zawisza (Jagiellonian University)

10:00 AM Compact domain approximation of the long-run impulse control with multiplicative functional

Impulse control provides a versatile framework for applying discrete-type interventions in continuous-time phenomena. This type of control can be applied e.g. to design foreign exchange intervention policies, specify optimal harvesting schemes, and model portfolios with transaction costs. In this talk we will discuss a compact domain approximation of the long-run impulse control problem for Feller-Markov processes with multiplicative optimality functional. The solution to the associated Bellman equation is constructed with the help of the Krein-Rutman theorem applied to the discrete time bounded state space version of the problem. The talk is based on a joint work with Łukasz Stettner [1].

[1] D. Jelito, Ł. Stettner, (2023), “Asymptotics of Impulse Control Problem with Multiplicative Reward”, Applied Mathematics and Optimization 88(24)

Speaker: Damian Jelito (Jagiellonian University)

9:30 AM → 10:30 AM MS 08: Mathematics and Magnetic Resonance Imaging: MS08-1

9:30 AM Model-based Cardiac T1-Mapping

The longitudinal relaxation time $T_1$ is an important biomarker in clinical cardiac MRI, e.g. for myocardial fibrosis. Conventional $T_1$ mapping is time-consuming and requires multiple breath holds. Therefore, we developed a sequence with a continuous radial readout which allows us to quantify $T_1$ within seconds. For reconstruction of the $T_1$ maps, the physical signal model of the MRI measurement sequence is incorporated as a constraint, which enables reconstruction with good image quality even from highly undersampled acquisition.

For a computationally efficient reconstruction, we approximate signal evolutions of the underlying nonlinear $T_1$ encoding model in a linear subspace spanned by four basis functions. A nonlinear forward model is set up, which maps the subspace coefficients and coil sensitivities to the acquired k-space data. Parallel imaging as nonlinear inversion is solved by the Iteratively Regularized Gauss Newton Method. Finally, the physical parameters of the signal model are pixel-wisely fitted to the coefficient maps in the subspace to obtain the $T_1$ map.

Speaker: Daniel Mackner (Graz University of Technology)

10:00 AM MRI in chemical engineering applications

In the field of chemical engineering, reactors play a vital role in processing and producing many goods However, their understanding is often limited by measurement access. Tomographic techniques can overcome these limits, with MRI being especially suitable. MRI can measure velocity and chemical composition in opaque systems and has been applied in the medical field extensively. While these capabilities are very promising, MRI faces challenges limiting its application such as sample size, low temporal resolution, and technique-specific properties.

At the Institute of Process Imaging at Hamburg University of Technology, our goal is to overcome these challenges. This talk tackles three challenges with MRI in chemical engineering.

• Size: Chemical reactors often rely on gravity. Therefore, a vertical system is best suited for measurement. However, most vertical systems only provide less than 7 cm of usable diameter. On the other hand, clinical scanners with higher diameters are oriented horizontally, limiting their capabilities. The TUHH vertical MRI scanner is a unique system designed to image pilot-scale reactors overcoming these limitations.

• Low temporal resolution: The temporal resolution of MRI has always been a challenge and only recently has improved significantly. Similar to the clinical field, parallel imaging and dedicated reconstruction enable temporal resolutions in the millisecond range.
  These make it possible to investigate dynamic systems. Especially challenging is the measurement of chemical compositions. Progress has been made to improve on these time-consuming measurements.

• Technique specific properties: MRI can deliver three-dimensional velocity fields. However, comparing these measurements to computational fluids simulations (CFD) often results in discrepancies. These can be the result of an unfair comparison, since MRI and CFD display different states of the system. Using a MR-Simulator (JEMRIS) and CFD-DEM simulations, the extent of these differences as well as the fairest way to compare can be obtained.

Speaker: Stefan Benders (Technische Universität Hamburg, Institut für Prozessbildgebung)

10:30 AM → 11:00 AM Coffee Break

11:00 AM → 12:00 PM MS 01: Optimal Control and Machine Learning: MS 01-4

11:00 AM On the continuity of the value function in reinforcement learning and optimal control

The value function plays a crucial role as a measure for the cumulative future reward an agent receives in both reinforcement learning and optimal control. It is therefore of interest to study how similar the values of neighboring states are, i.e. to investigate the continuity of the value function. We do so by providing and verifying upper bounds on the value function's modulus of continuity. Additionally, we show that the value function is always Hölder continuous under relatively weak assumptions on the underlying system.

Speaker: Hans Harder (University of Paderborn)

11:30 AM Physics-informed neural networks for non-smooth PDE-constrained optimization problems

We study the application of well-known physics-informed neural networks (PINNs) for solving non-smooth PDE-constrained optimization problems. First, we consider a class of PDE-constrained optimization problems where additional nonsmooth regularization is employed for constraints on the control or design variables. For solving such problems, we combine the alternating direction method of multipliers (ADMM) and PINNs and propose the ADMM-PINNs algorithmic framework, which unties the PDE constraints and the nonsmooth regularization terms for iterations. Accordingly, at each iteration, one of the resulting subproblems is a smooth PDE-constrained optimization which can be efficiently solved by PINNs, and the other is a simple nonsmooth optimization problem which usually has a closed-form solution or can be efficiently solved by various standard optimization algorithms or pre-trained neural networks. Various numerical results are reported to validate the effectiveness and efficiency of the proposed ADMM-PINNs methods.

Speaker: Yongcun Song

11:00 AM → 12:30 PM MS 03: Recent trends in control and numerics of port-Hamiltonian systems: MS03-1

11:00 AM Structure preserving time discretization of port-Hamiltonian systems

Port-Hamiltonian systems are becoming increasingly important in the modelling of physical systems. The key feature of this class of systems is the coupling of different subsystems using energy as the “lingua franca”. Although obtaining structure preserving space discretizations is quite straightforward, structured time discretizations of pH systems are more challenging. For the latter, the main goal is to have an energy balance for the time-discrete system that resembles the energy balance of the original model. This is especially challenging for nonlinear systems.

In this talk, we present a structure preserving scheme based on a Petrov-Galerkin-type procedure that is suitable for nonlinear systems. The approach uses a piecewise polynomial ansatz to approximate the trajectory of the pH system, which allows for an arbitrary order of convergence. We show that the scheme leads to the satisfaction of a discrete-time energy balance and present an a posteriori estimate for the approximation error. Finally, we illustrate the effectiveness of the approach with numerical examples.

Speaker: Attila Karsai (TU Berlin)

11:30 AM High-order operator splitting methods for linear port-Hamiltonian systems

The lecture deals with numerical methods for solving port-Hamiltonian systems. The focus is on operator splitting methods. The aim is to derive high-order methods that preserve the port-Hamiltonian properties. Splitting methods with an order of three and higher have negative step sizes. As a result, the dissipation inequality is no longer preserved. Remedy create force-gradient methods. With the help of force-gradient terms, it is possible to construct fourth-order methods that only have positive step sizes and satisfy the dissipation inequality. Finally, the case of sixth order methods is explained.

Speaker: Marius Mönch (Trier University - Department IV)

12:00 PM Jet space extensions of infinite-dimensional Hamiltonian systems

Infinite-dimensional Hamiltonian systems offer an energy-based approach to model complex physical phenomena, appearing e.g. in fluid dynamics or mechanics. They are defined via a formally skew-symmetric Hamiltonian operator and are associated with a non-quadratic Hamiltonian energy function. In various applications, however, the Hamiltonian function depends on spatial derivatives of the state. This characteristic prevents a direct description of the system dynamics using geometric structures, as in the framework of boundary port-Hamiltonian systems. The underlying reason is that the boundary port variables, which are necessary to derive an energy balance, are not straightforward to deduce due to the strong intertwinement of energy-storing components modeled by a Stokes-Lagrange structure, and energy-routing elements modeled by a Stokes-Dirac structure.

In this talk, we propose a method to reformulate infinite-dimensional Hamiltonian systems on one-dimensional spatial domains as boundary port-Hamiltonian systems by embedding the system into the (higher-dimensional) jet space, that is, augmenting the state variable with its spatial derivatives. This reformulation enables the application of the comprehensive theory of boundary port-Hamiltonian systems including control access.

Speaker: Till Preuster (Technische Universität Ilmenau)

11:00 AM → 12:30 PM MS 06: Recent advances in PDE-constrained optimization: MS 06-1

11:00 AM Optimal Control of elliptic PDEs with Wasserstein Regularization

We consider an elliptic optimal control problem with a control in the space of regular Borel measures. The Tikhonov regularization term is given by the Wasserstein-$p$-distance , $p \in [1, \infty)$, to a given prior. We establish first-order necessary optimality conditions using the convex subdifferential of the Wasserstein-$p$-distance. These conditions couple the adjoint state with the Kantorovich potential as solution of the dual Kantorovich problem. By employing this coupling, smoothness properties of the optimal control as well as structural properties of its support can be shown depending on the choice of $p$.

Speaker: Christian Meyer (TU Dortmund)

11:30 AM Optimal control of rate-independent systems with non-convex energy

This talk deals with an optimal control problem, where the state variable is given as a parametrized balanced viscosity solution of a rate-independent system with non convex energy.
Under certain assumptions on the data one can prove the existence of globally optimal solutions for external loads in $H^1(0,T)$.
Moreover, we investigate the approximability of optimal solutions by viscous regularized problems.
The underlying analysis is based on an approximation argument including an additional penalty term besides viscous regularization.

Speaker: Merlin Andreia (TU Dortmund)

12:00 PM The Pontryagin maximum principle for the optimal control of coefficients of an elliptic differential operator

We consider optimal control problems where the control acts in the coefficient of the main part of the elliptic differential operator. We develop expansions of the cost functional with respect to perturbations of the control by characteristic functions. In comparison to standard Frechet derivatives in $L^\infty$, an additional term appears, which is related to the so-called polarization tensor. We prove that the Pontryagin maximum principle is necessary for local optimality. We discuss implications of the maximum principle. In particular, we show that certain classes of problems are unsolvable.

Speaker: Daniel Wachsmuth

11:00 AM → 12:30 PM MS 09: Stochastic Modeling and Control: MS 09-2

11:00 AM Reinforcement Learning Methods for Risk-Sensitive Investment Management

We investigate the benefits of relating reinforcement learning (RL) with risk-sensitive control. Our starting point is the duality between free energy and relative entropy, see e.g. Dai Pra et al. (1996). It establishes an equivalence between risk-sensitive control and standard stochastic control problems with an entropy regularization term.

This approach has two major advantages:
i) it does not require a preliminary change of measure `a la Kuroda & Nagai (2002));
ii) it is naturally consistent with the use of a regularization/penalization term in the literature that connects reinforcement learning with stochastic control, e.g. Wang et al. (2019). In this sense, it also allows for a risk-sensitive interpretation of the entropy regularization in RL.

We furthermore show how this connects to the existing literature on risk-sensitive investment management (Kuroda & Nagai, 2002; Davis & Lleo, 2008, 2020, 2021), whereby cases with unknown parameters or with partial observation showcase the advantages of reinforcement learning methods.

Speaker: Sebastien Lleo (NEOMA Business School)

11:30 AM Discrete-time risk sensitive portfolio optimisation

In this talk we will consider the problem of discrete-time risk-sensitive portfolio optimization over a long time horizon. In particular, the relationship between ergodic assumptions and the existence of a solution to a suitable Bellman equation will be discussed. This will include various portfolio optimisation frameworks linked to i.i.d. settings, the presence of proportional transaction costs, unbounded reward functions, and interactions between averaged and discounted problems in the finite setup.

Speaker: Marcin Pitera (Jagiellonian University)

12:00 PM Financial markets with concave transaction costs

In the talk we consider discrete time financial markets with concave transaction costs. This means that bid and ask prices depend on the volume of transaction in such a way that when we buy more assets we pay smaller (proportionally) transaction costs, while when we sell more assets we pay less for proportional transaction costs. Such situation appears usually on currency markets and real estate markets (for more expensive real estates transaction costs paid as a certain percentage of the transaction volume usually diminish). In the case of concave transaction costs so called solvent sets (the sets of non-negative positions) are not convex and we have problems to find proper mathematical tools. In the talk sufficient conditions for absence of so called strong arbitrage are formulated. The results overcome a gap which appeared in the paper [1]. The presentation is based on the paper [2].

References:
[1] E. Lepinette, T. Tran, Arbitrage theory for non convex financial market models, Stochastic processes and their appl. 127 (2017), 3331--3353,
[2] A. Rygiel, L. Stettner, On general financial markets with concave transaction costs, in preparation.

Speaker: Agnieszka Rygiel (Krakow University of Economics)

11:00 AM → 12:30 PM MS 10: Inverse Problems for Partial Differential Equations: MS 10-3

11:00 AM The temporal domain derivative and shape reconstruction in inverse acoustic scattering

Domain derivatives have been studied for a variety of time-harmonic scattering problems featuring different partial differential equations, boundary conditions and geometrical configurations.
The aim of this presentation is to establish the temporal domain derivative for the acoustic wave equation when a sound-soft scattering object is present.
In our analysis we proceed through the Laplace domain, in which we derive bounds for the frequency-domain shape derivative expressed in terms of powers of the frequency.
Performing an inverse Laplace transform turns these powers into time regularity requirements guaranteeing the existence of the temporal domain derivative.
In our inverse problem the aim is to reconstruct the scattering object from temporal measurements of the scattered wave at a finite set of observation points that are situated away from the scattering object.
For this purpose we employ a Gauß-Newton scheme, in which we use the Runge-Kutta convolution quadrature method to approximate both the forward map and the temporal domain derivative. This guarantees an efficient time integration scheme.
We provide numerical examples for the two-dimensional wave equation that highlight the efficacy of our approach.

Speaker: Marvin Knöller

11:30 AM Hybrid Gaussian Beam Pseudo-Spectral Method for Efficient Wave Propagation in PAT

The forward and adjoint problems in photoacoustic tomography can be modelled as an initial value and a time varying source problem for the free space wave equation. Despite the advances made in recent years (parallel interrogation with up to 64 beams), the data acquisition time in state-of-the-art PAT scanners is still a bottle-neck resulting in sparse, limited angle data. The solution of inverse problems with incomplete data necessitates iterative methods involving repeated calls to the forward and adjoint solvers, which is the most compute intensive part of the process. Inspired by the Multiscale Gaussian Beam decomposition proposed by Qian and Ying (Multiscale Modeling & Simulation, 8 (2010), pp. 1803–1837), we devise an efficient hybrid wave solver, leveraging Gaussian Beams for efficient and highly parallel propagation of high frequency components of the solution, and a pseudo-spectral method for accurate propagation of the low frequency components. We discuss the accuracy and performance of our method on an example of the forward problem in PAT.

Speaker: Mr Elliott Macneil (UCL)

12:00 PM Inverse problems for active matter

Many processes in cells are driven by the interaction of multiple proteins, for example cell contraction, division or migration. Two important types of proteins are actin filaments and myosin motors. Myosin is able to bind to and move along actin filaments with its two ends, leading to the formation of a dynamic actomyosin network, in which stresses are generated and patterns may form. Droplets containing an actomyosin network serve as a strongly simplified model for a cell, which are used to study elemental mechanisms. We are interested in determining the parameters that characterize this active matter, i.e., active forces that cause the dynamics of an actomyosin network, represented by the flow inside the actomyosin droplet, as well as the local viscosity. We use the Stokes equation with a spatially varying viscosity to model the flow caused by the activity (active forces) of the actomyosin network. A goal in biophysics is the identification of such active forces from measurements of the resulting flow field, leading to a parameter identification problem for the Stokes equation that is discussed in this talk in connection to the experimental setup.

Speaker: Anne Wald (University of Göttingen)

12:30 PM → 2:00 PM Lunch

2:00 PM → 4:00 PM Plenary Talk

2:00 PM Smoothed circulant embedding and applications in multilevel Monte Carlo methods

Parameters in mathematical models for physical processes are often impossible to determine fully or accurately, and are hence subject to uncertainty. By modelling the input parameters as stochastic processes, it is possible to quantify the uncertainty in the model outputs. In this talk, we employ the multilevel Monte Carlo (MLMC) method to compute expected values of quantities of interest related to partial differential equations with random coefficients. We make use of the circulant embedding method for sampling from the coefficient, and to further improve the computational complexity of the MLMC estimator, we devise and implement the smoothing technique integrated into the circulant embedding method. This allows to choose the coarsest mesh on the first level of MLMC independently of the correlation length of the covariance function of the random field, leading to considerable savings in computational cost.

Speaker: Prof. Aretha Teckentrup (University of Edinburgh)

3:00 PM Qualitative properties of minimizers of Total-Variation regularized problems

The total variation has been successful as a regularizer for inverse problems in imaging, thanks to its ability to preserve discontinuities (edges) and its relative simplicity (convexity). Even if largely outdated by deep learning based method, it still can be useful in some regimes (low noise, large scale images). This talk is about the preservation of edges in total-variation based denoising. We revisit old proofs which show in some settings that no spurious edges are created by this apporach. Our new approach, much simpler and natural than the previous, applies to more settings (color/multispectral data, some higher order models); on the other hand, proving more precise regularity still remains a challenge.

This is joint work with Michał Łasica, Warsaw.

Speaker: Prof. Antonin Chambolle (CEREMADE in Dauphine / PSL university)

4:00 PM → 4:30 PM Coffee Break

4:30 PM → 6:00 PM MS 03: Recent trends in control and numerics of port-Hamiltonian systems: MS03-2

4:30 PM Regularization and stabilization of port-Hamiltonian descriptor systems via output feedback

Regularization and index reduction for singular linear port-Hamilonian descriptor systems via output feedback is discussed. When the system is regularized and has index at most one, then the system is stable and passive, but not necessarily asymptotically stable and strictly passive. It is then shown how output feedback can be used to make the system (robustly) asymptotically stable and strictly passive.

Speaker: Volker Mehrmann (TU Berlin)

5:00 PM Optimal control of port-Hamiltonian systems

The framework of port-Hamiltonian (pH) systems allows to deduce structured models for physical systems from various domains. In recent work we have explored how the pH structure can be exploited in the analysis optimal control problems. Specifically, we consider the analysis of minimizing the energy supplied to the system while ensuring a set-point transition. We show that the pH structure allows to exploit the Hamiltonian structure of the optimality system in particular manner. Our findings are supported by numerical results for thermodynamic and mechanical examples.

Speaker: Timm Faulwasser (TU Dortmund)

5:30 PM A Toolbox for the Automatic Generation of Port-Hamiltonian Models for Mechanical Structures

Adaptive structures are ultra-lightweight structures with actuation distributed among the structural elements. They enable material savings in high-rise construction of about 50%. Energy-based methods offer advantages in modeling for coupling the mechanical structure with actuators from another domain, such as hydraulic, and also for the design of an energy-based controller or state estimator. However, these high-dimensional structures are typically modelled using a finite element (FE) approach. To combine the advantages of energy-based modeling and of the FE-approach, we provide a toolbox utilizing our results from discretizing distributed PH-models of structural elements using the partitioned finite element method (PFEM). This talk will illustrate these mathematical basics on a simple example and showcase the application of the toolbox for the adaptive high-rise demonstrator D1244 on the campus of the University of Stuttgart. The toolbox is available at https://github.com/awarsewa/ph_fem/.

Speaker: Amelie Zeller

4:30 PM → 6:00 PM MS 04: Correlation-based passive imaging and optimal experimental design: MS 04-4

4:30 PM Tractable optimal experimental design using transport maps

We present an approach for optimal experimental design (OED) for Bayesian inverse problems characterized by non-Gaussian, intractable posteriors. Our transport-map-based approach is versatile, accommodating various optimality criteria, design types, and prior distributions. In this talk, we highlight the key aspects of our method with a focus on the Bayesian D-optimality criterion, which aims to maximize the expected information gain from prior to posterior. A crucial tool for our approach is the Knothe-Rosenblatt rearrangement, which facilitates efficient sampling from conditional distributions that appear in many optimality criteria. We construct this map via a tensor train surrogate to the intractable target density. We also discuss extensions of our approach to sequential design problems and supplement our discussion with numerical examples.

Speaker: Karina Koval (Heidelberg University)

5:00 PM Quasi-Monte Carlo methods for Bayesian optimal experimental design

Bayesian optimal experimental design (OED) seeks to maximize the expected information gain for the reconstruction of unknown quantities in an experiment by optimizing the placement of measurements. The objective function in the resulting optimization problem contains a high-dimensional integral with respect to the posterior distribution. We will approximate these high-dimensional integrals using tailored quasi-Monte Carlo methods to reduce the computational burden associated with Bayesian OED problems governed by partial differential equations. Numerical experiments showcase the theoretical results.

Speaker: Vesa Kaarnioja (Universität Potsdam)

5:30 PM Efficient nested integration estimators for optimal experimental design

Measuring the expected information gain (EIG) of an experiment allows for comprehensive design optimization. Efficiently estimating the EIG is crucial when data are scarce or costly to obtain. We propose several estimators combining the randomized quasi-Monte Carlo method with Laplace-based importance sampling, and showcase their efficiency both theoretically and via numerical examples.

Speaker: Arved Bartuska

4:30 PM → 5:30 PM MS 06: Recent advances in PDE-constrained optimization: MS 06-2

4:30 PM Adaptive Trust Region Reduced Basis Methods for Parameter Identification Problems

In this talk, we are concerned with model order reduction in the context of iterative regularization methods for the solution of inverse problems arising from parameter identification in elliptic partial differential equations. Such methods typically require a large number of forward solutions, which makes the use of the reduced basis method attractive to reduce computational complexity.

However, the considered inverse problems are typically ill-posed due to their infinite-dimensional parameter space. Moreover, the infinite-dimensional parameter space makes it impossible to build and certify classical reduced-order models efficiently in a so-called offline phase. We thus propose a new algorithm that adaptively builds a reduced parameter space in the online phase. The enrichment of the reduced parameter space is naturally inherited from the Tikhonov regularization within an iteratively regularized Gauss-Newton method.

Finally, the adaptive parameter space reduction is combined with a certified reduced basis state space reduction within an adaptive error-aware trust region framework. Numerical experiments are presented to show the efficiency of the combined parameter and state space reduction for
inverse parameter identification problems with distributed reaction or diffusion
coefficients.

Speaker: Michael Kartmann (Uni Konstanz)

5:00 PM A least-squares space-time approach for parabolic equations

We consider a least squares formulation of a linear parabolic equation in spaces with natural regularity. As a consequence the formulation contains the Riesz isomorphism.
The discrete approach uses space-time finite elements and a suitable approximation of the Riesz isomorphism. Using finite elements that are separable with respect to space and time
the final fully discrete representation has the form of a generalized Lyapunov equation. The numerical solution of this system requires a taylored approach. Finally we discuss the use of reduced basis methods for our problem.

Speaker: Christian Kahle

4:30 PM → 5:30 PM MS 10: Inverse Problems for Partial Differential Equations: MS 10-4

4:30 PM Bi-level iterative regularization for inverse problems in nonlinear PDEs

We investigate the ill-posed inverse problem of recovering unknown spatially dependent parameters in nonlinear evolution PDEs. We propose a bi-level Landweber scheme, where the upper-level parameter reconstruction embeds a lower-level state approximation. This can be seen as combining the classical reduced setting and the newer all-at-once setting, allowing us to, respectively, utilize well-posedness of the parameter-to-state map, and to bypass having to solve nonlinear PDEs exactly. Using this, we derive stopping rules for lower- and upper-level iterations and convergence of the bi-level method. We discuss application to parameter identification for the Landau-Lifshitz-Gilbert equation in magnetic particle imaging.

Speaker: Tram Nguyen (Max Planck Institute for Solar System Research)

5:00 PM A stability result for the identification of a displacement discontinuity jump on linear elasticity equations

This work presents an inverse problem where we seek to recover the discontinuity jump of the displacements field that verifies a linear elasticity equation, from measurements of the displacement field or traction field on a subdomain of the bordary. This inverse problem allows us to study subduction earthquakes, which are of great importance to the geophysical community.
To obtain the stability result, the problem is rewritten using a mixed variational formulation with a unique solution. By applying Carleman inequalities appropriately, it is possible to obtain a new energy estimate that, by adding an additional condition, makes it possible to obtain the desired estimate.
Some numerical tests will be presented that allow us to complement the theory presented simulating a realistic case of a subduction earthquake on the coast of Chile.

References
1. Oleg Yu. Imanuvilov and Masahiro Yamamoto. An inverse problem and an observability inequality for the Lamé system with stress boundary condition. Applicable Analysis, 88(5):711–733, May 2009.
2. Jorge Aguayo and Rodolfo Araya. A priori error estimates for a coseismic slip optimal control problem, 2024. Submitted for publication to Applied Numerical Mathematics.

Speaker: Dr Jorge Aguayo Araneda (Centro de Modelamiento Matemático - Universidad de Chile)

Wednesday, August 14

9:00 AM → 10:30 AM MS 06: Recent advances in PDE-constrained optimization: MS 06-3

9:00 AM SQP Method for Hyperbolic PDE-Constrained Optimization in Acoustic Full Waveform Inversion

This talk presents recent results on the SQP method for hyperbolic PDE-constrained optimization in acoustic full waveform inversion. The analysis of the SQP method is mainly challenging due to the involved hyperbolicity and second-order bilinear structure. This notorious character leads to undesired effects of regularity loss in the SQP iteration calling for a substantial extension of developed parabolic techniques. We propose and explore a novel strategy for the well-posedness and convergence analysis of the SQP method based on the use of a smooth-in-time initial condition, a tailored self-mapping operator, and a two-step estimation process along with Stampacchia's method. Our final theoretical result is the R-superlinear convergence of the SQP method.

Speaker: Irwin Yousept (University Duisburg-Essen)

9:30 AM Image Registration Using Optimal Control of a Linear Hyperbolic Transport Equation

Image registration is crucial in many imaging applications such as medical imaging or computer vision. The goal of finding a suitable transformation between two images poses similar restrictions and requirements on the set of admissible transformations as shape optimization problems. In the scope of this talk, we build on an approach that models image registration as an optimization problem that is constrained by a linear hyperbolic transport equation. We use a higher-order discontinuous Galerkin finite element method for discretization and motivate the numerical upwind scheme and its limitations from the continuous weak space-time formulation of the transport equation. Moreover, we build on recent theoretical results to model the optimization problem. To discuss the potential of the proposed algorithm, we apply it to patient specific brain mesh generation from magnetic resonance images (MRI). This can be a time consuming task and require manual corrections, e.g., for meshing the ventricular system or defining subdomains. The idea is to use the registration of an input MRI to a respective target in order to obtain a new mesh from a high-quality template mesh.

Speaker: Johannes Haubner (University of Graz)

10:00 AM Optimal Control of the Generalized Riemann Problem for Hyperbolic Systems of Conservation Laws

In this talk, we analyze optimal control problems for quasilinear strictly hyperbolic systems of conservation laws where the control is the initial state of the system. The problem is of interest, for example, in the context of fluid mechanics or traffic flow modelling. Similar problems for scalar conservation laws have already been studied. However, the case of hyperbolic systems is more involved due to the coupling of the characteristic fields.

We begin our analysis by considering the Generalized Riemann Problem, which has a piecewise smooth initial state with exactly one discontinuity. This is a natural choice since it is well known that solutions to hyperbolic conservation laws generally develop discontinuities even for smooth data. For piecewise $C^1$ initial data we obtain the existence, uniqueness and stability of an entropy solution by a careful fixed point argument built on the associated Riemann Problem with piecewise constant initial states. The construction yields insights into the structure and regularity of the solution and provides a foundation to derive differentiability results of the control-to-state mapping.

The entropy solution is piecewise $C^1$. Its smooth parts are separated by $C^2$ curves which are either shock curves or boundaries of rarefaction waves. In a subsequent step, we show that these curves depend differentiably on the initial state. This allows the transformation to a fixed space-time domain as a reference space. In this reference space, we can show that the transformed solution depends differentiably on the initial state in the topology of continuous functions. For this, a detailed knowledge of the structure of the solution and the behaviour of the shock curves is crucial. As an immediate consequence, the differentiability of tracking type functionals for the optimal control problem follows.

Speaker: Jannik Breitkopf (TU Darmstadt)

9:00 AM → 10:30 AM MS 08: Mathematics and Magnetic Resonance Imaging: MS08-2

9:00 AM Quantitative MRI as a non-linear tomography problem: from mathematical principles to clinical demonstration

Quantitative Magnetic Resonance Imaging (MRI) is based on a two-steps approach: estimation of the magnetic moments distribution inside the body, followed by a voxel-by-voxel quantification of the human tissue properties. This splitting simplifies the computations but poses several constraints on the measurement process, limiting its efficiency. Instead, we can perform quantitative MRI as a one step process; signal localization and parameter quantification are simultaneously obtained by the solution of a large scale nonlinear inversion problem based on first-principles. As a consequence, the constraints on the measurement process can be relaxed and acquisition schemes that are time efficient and widely available in clinical MRI scanners can be employed.

In this talk, the mathematical principles underlying the nonlinear inversion formulation of quantitative MRI are outlined, computational challenges associated with numerically solving such a large scale problem are discussed and results from clinical demonstrator studies are presented.

Speaker: Oscar van der Heide (University Medical Center Utrecht)

9:30 AM Assessment of Deep Learning-based Reconstruction with Imperfect Ground Truth for MRCP

Magnetic resonance cholangiopancreatography (MRCP) is a non-invasive imaging technique to visualize the hepatobiliary system. However, acquiring MRCP using a triggered 3-D T2-weighted turbo spin echo sequence causes prolonged scan time and often provides undiagnostic image quality. Therefore, we aimed to accelerate MRCP acquisition using deep learning (DL)-based reconstruction.

We acquired conventional two-fold accelerated MRCP on 3T scanners (Siemens Healthineers, Erlangen) as used in clinical routine. Then, we trained a variational network (VN) [1] with two-fold GRAPPA reconstruction as ground truth and retrospective six-fold undersampling as input. We compared our method with parallel imaging [2], compressed sensing [3], and a self-supervised learning method, SSDU (self-supervised learning via data undersampling) [4], designed for situations lacking fully sampled ground truth. We evaluated reconstructions based on peak signal-to-noise ratio (PSNR) and structural similarity (SSIM). Furthermore, we tested our method with prospective six-fold undersampling to reflect real-world clinical applications and applied this approach to 0.55T MRCP to assess its adaptability.

In summary, our method demonstrated superior performance in reconstructing both prospectively and retrospectively undersampled data, yielding higher metric scores and improved image quality. It also effectively reduced background noise in images acquired at 0.55T without compromising detail.

Reference
1. K. Hammernik et al., "Learning a variational network for reconstruction of accelerated MRI data," MRM, 2018.
2. K. P. Pruessmann et al., "Advances in sensitivity encoding with arbitrary k-space trajectories," MRM, 2001.
3. M. Lustig et al., "Sparse MRI: The application of compressed sensing for rapid MR imaging," MRM, 2007.
4. B. Yaman et al., "Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data," MRM, 2020.

Speaker: Jinho Kim (Friedrich-Alexander-Universität Erlangen-Nürnberg)

10:00 AM Robustness of Deep Learning for Accelerated MRI: Benefits of Diverse Training Data

Deep learning based methods for image reconstruction are state-of-the-art for a variety of imaging tasks. However, neural networks often perform worse if the training data differs significantly from the data they are applied to. For example, a network trained for accelerated magnetic resonance imaging (MRI) on one scanner performs worse on another scanner. In this work, we investigate the impact of the training data on the model's performance and robustness for accelerated MRI. We find that models trained on the combination of various data distributions, such as those obtained from different MRI scanners and anatomies, exhibit robustness equal or superior to models trained on the best single distribution for a specific target distribution. Thus training on diverse data tends to improve robustness. Furthermore, training on diverse data does not compromise in-distribution performance, i.e., a model trained on diverse data yields in-distribution performance at least as good as models trained on the more narrow individual distributions. Our results suggest that training a model for imaging on a variety of distributions tends to yield a more effective and robust model than maintaining separate models for individual distributions.

Speaker: Reinhard Heckel (TUM)

9:00 AM → 10:30 AM MS 09: Stochastic Modeling and Control: MS 09-3

9:00 AM Absolute Continuity for Rosenblatt Measures

A Rosenblatt measure denotes the measure for a Rosenblatt process that is a non-Gaussian process that can be explicitly described as a product of two Wiener-Itô stochastic integrals with suitable singular kernels. These Rosenblatt processes have a useful stochastic calculus that includes an explicit change of variables formula. Given the usefulness of absolute continuity for Wiener measures, it is natural to consider absolute continuity questions for various stochastic transformations of a Rosenblatt process. Explicit expressions for some Radon-Nikodym derivatives are given. Recalling various transformations of a Wiener measure by a Radon-Nikodym derivative, the results for Rosenblatt measures can be quite useful for various stochastic problems.

Speaker: Tyrone E. Duncan (Department of Mathematics, University of Kansas)

9:30 AM Interdisciplinary Research Addressing New Challenges: The Central Role of Stochastic Systems and Control

In 2017, the US National Science Foundation (NSF) announced 10 Big Ideas for Future Investment. These research ideas, such as ”Harnessing the Data Revolution” or ”Future of Work at the Human Technology Frontier”, all require expertise from multiple disciplines to come together to address specific problems that are important in our society. One of ideas, ”Growing Convergence Research” is explicitly about expanding our ability to conduct multi and interdisciplinary research. ”The goal was to motivate dynamic, fundamental, interdisciplinary research building on a theme that science is strongest when science works together.” Certainly, with advances in computing and sensor development, stochastic systems, control and adaptive control will play a central role in much of that multi and interdisciplinary research. This talk will focus on advances in noise modeling in stochastic systems, control and adaptive control.

Speaker: Prof. Bozenna Pasik-Duncan (Departments of Mathematics, AE and EECS; University of Kansas, Lawrence, Kansas, USA)

10:00 AM Asymptotics and stability of long run stochastic control problems

In the talk for discrete time controlled Markov processes dependence of the long run functionals: average reward per unit time and risk sensitive, with respect to Markov controls, functions in the functional and risk factor (in the case of risk sensitive functionals) will be studied. It is shown that under nice ergodic assumptions we have suitable continuity properties. Such properties justify the use of Monte Carlo methods to look for nearly optimal controls (in particular when dimension of the model is relatively large). They play also crucial role when we study long run problems with general discounting and want to show that optimal control for long run undiscounted functionals is nearly optimal control for generally discounted long run problems. The talk will be an extension of the papers [1] and [2].

References:

[1] L. Stettner, Stability of long run functionals with respect to stationary Markov controls, submitted to CDC 2024,

[2] L. Stettner, Long run stochastic control problems with general discounting, to appear in AMO, arXiv:2306.14224

Speaker: Prof. Lukasz Stettner (Institute of Mathematics PAS)

10:30 AM → 11:00 AM Coffee Break

11:00 AM → 12:30 PM MS 06: Recent advances in PDE-constrained optimization: MS 06-4

11:00 AM Generalized derivatives for the solution operator of the obstacle problem and error estimates for numerical approximations

We derive and present error estimates for numerical approximations of a particular Clarke subgradient for reduced objective functions arising in the optimal control of the obstacle problem. The corresponding generalized derivative of the solution operator of the obstacle problem is a solution operator of a Dirichlet problem on the complement of the strictly active set. Using finite element solutions of the obstacle problem, we construct discrete and convergent approximations of this set. To show that our approximations are suitable and convergent, a detailed study of the topological structure of the strictly active set under appropriate assumptions is necessary. Based on the smaller approximation, we solve the Dirichlet problem and obtain an upper bound for the error using the larger approximation. This upper bound converges to zero. We present numerical examples to test our estimates.

Speaker: Prof. Stefan Ulbrich (TU Darmstadt)

11:30 AM Robust Parameter and Shape Optimization of Electrical Machines with Isogeometric Analysis

In electric machine design efficient methods for the optimization of geometry and associated parameters are essential. Nowadays, it is necessary to handle uncertainty caused by manufacturing or material tolerances. In this work we propose a robust optimization approach to handle uncertainty in the design of a 3-phase, 6-pole Permanent Magnet Synchronous Motor (PMSM). The geometry is constructed in a two-dimensional framework, employing Isogeometric Analysis (IGA) to enable flexible shape optimization. The main contributions of this research are twofold. First, we integrate shape optimization with parameter optimization to enhance the performance of PMSM designs. Second, we use robust optimization which creates a min-max problem to ensure the motor maintains its performance when facing uncertainties. To solve this bilevel problem, we work with the maximal value functions of the lower level maximization problems and apply a version of Danskin's Theorem for the computation of generalized derivatives. Additionally, the adjoint method is employed to efficiently solve the lower level problems with gradient based optimization. The paper concludes by presenting numerical results.

Speaker: Theodor Komann (TU Darmstadt)

12:00 PM Coefficient Control for Variational Inequalities

In this talk, we consider the introduction of a control variable into
the coefficients of the variational inequality constraint of an
optimal control problem. To this effect, we discuss optimality
conditions for a problem governed by an obstacle problem with control in the coefficients.
Since the obstacle problem acts as a complementarity constraint, it is known, that standard constraint qualifications do not apply. Further, we will utilize a regularization approach to address the lack of Gateaux differentiability inherent to the obstacle problem. The novelty of this talk will be the use of H-convergence techniques in conjunction with such a regularization approach to discuss optimality conditions for a problem subject to, coefficient controlled, variational inequality constraints.

Speaker: Nicolai Simon

11:00 AM → 12:30 PM MS 08: Mathematics and Magnetic Resonance Imaging: MS 08-3

11:00 AM Mathematical background of ESPIRiT: ESPIRiT versus MOCCA

Recently, we have proposed a new model-based coil calibration (MOCCA) algorithm to reconstruct the coil sensitivities and the magnetization image from the given (incomplete) measurements. This method employs the assumption that the coil sensitivities are smooth functions which can be represented using bivariate trigonometric polynomials of small degree while the magnetization image is only assumed to be a compactly supported distribution. The MOCCA algorithm provides perfect reconstruction results if the model assumptions are satisfied. Moreover, it has a low computational complexity and fits real MRI data sufficiently well such that it is applicable in practice. In this talk, we present the close connection between the celebrated ESPIRiT algorithm and MOCCA thereby showing that MOCCA provides the mathematical background of ESPIRiT. This new insight provides us the with the opportunity to search for improved sensitivity models which are more appropriate for parallel MRI reconstructions thereby still allowing fast reconstruction procedures.

Speaker: Gerlind Plonka (Universität Göttingen)

11:30 AM Phase distribution graphs for differentiable and efficient simulations of arbitrary MRI sequences

Introduction

We present an analytical Bloch simulation approach for arbitrary MRI sequence simulation called Phase Distribution Graphs. It is a general implementation of the Extended Phase Graph (EPG) concept, based on the Fourier-domain Bloch equation, but with arbitrary timing, and including the exact contribution of dephased states resulting from spatial encoding and T2’ relaxation effects. In contrast to EPG, which was limited to echo amplitudes only, this allows calculation of full echo shapes. Our Pytorch implementation provides full differentiability in all input parameters allowing gradient descent optimization. A major problem of phase graphs, the generation of an „astronomical number of states“ is solved by an efficient state selection algorithm. The simulation compares well to results of conventional Bloch simulations with quasi-random isochromat distribution, which it outperformed in simulation time by at least one order of magnitude. Different sequences and their artifacts are analyzed and improved, underlining that Phase Distribution Graphs allow efficient simulation and optimization of arbitrary MRI sequences, which was previously only possible via high isochromat counts.

Theory

In contrast to EPG \footnote{Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes - pure and simple. J Magn Reson Imaging. 2015 Feb;41(2):266-95. doi: 10.1002/jmri.24619.}, which describes magnetization states as plane waves $e^{i\mathbf{k}\cdot\mathbf{r}} $, we propose to modify the magnetization to be represented by a more complex state, but still a single state $ F^ {\hat{e} }_{k,\tau} $:

$M^ {\hat{e}}(\mathbf{r},\omega) = F^ {\hat{e}}_{k,\tau} \cdot e^{i\mathbf{k}\cdot\mathbf{r}} \cdot e^{i\tau\omega} \cdot W(\omega,\mathbf{r}) \cdot V(\mathbf{r}) $

Including the spatial distribution V (voxel positions and shape) and the spectral distribution W (T2‘ dephasing).

Assuming a sinc voxel shape for V, and a Cauchy-Distribution ($\Delta\omega_0$, T2‘) for W the full simulated measurable MRI signal is given by the sum of all + states, integrated over space $\mathbf{r}$ and all frequencies $\omega$ leading to

$S = \sum_{\nu} \sum_{k,\tau} F^ {+}_{k,\tau} \cdot (e^{i\Delta\omega_0\tau} \cdot e^{-|\tau|/T'_2}) \cdot \left( e^{i\mathbf{k} \cdot \mathbf{r}_{{\nu} } } \cdot \Theta \left(\mathbf{k}-\mathbf{k}_{{\nu} } \right) \right) $

, i.e., the sum over all $k$-and $\tau$-dephased +-states of all voxels $\nu$. Here $\Theta$ is the Heaviside function limiting k to the first k-space.

A single pre-pass calculation of this signal equation allows us to identify the most important states of a certain MRI sequence, and we can define by a threshold the trade-off between duration and accuracy of the simulation.

Results

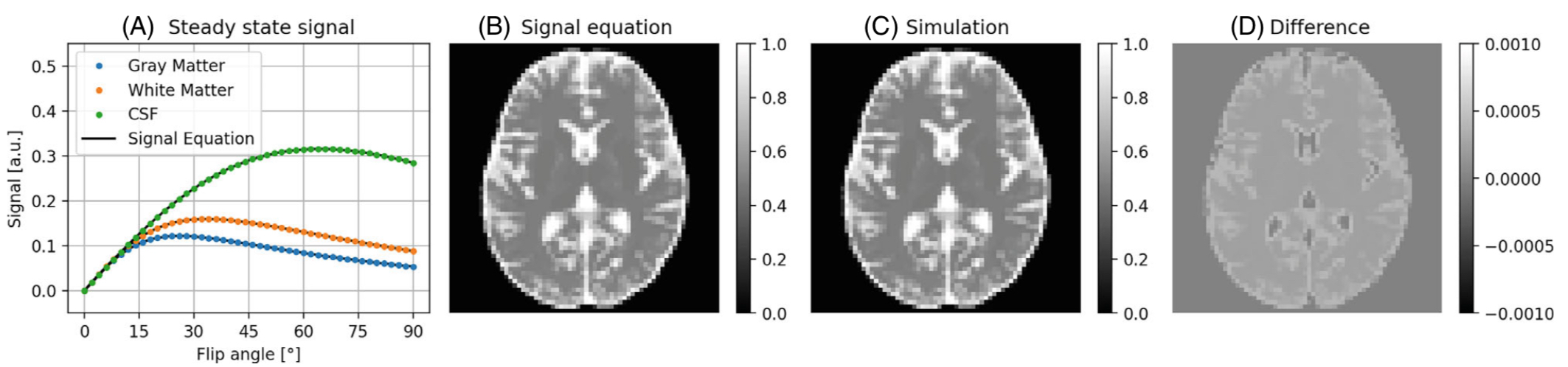
Figure 1 shows the match between our simulation and the analytical solution of a bSSFP sequence. Figure 2 shows comparison to an isochromat solution in the case of 90 degree SSFP with a large fraction of dephased magnetization. The run time analysis shows that PDG outperforms conventional Bloch simulations in such cases by two orders of magnitude.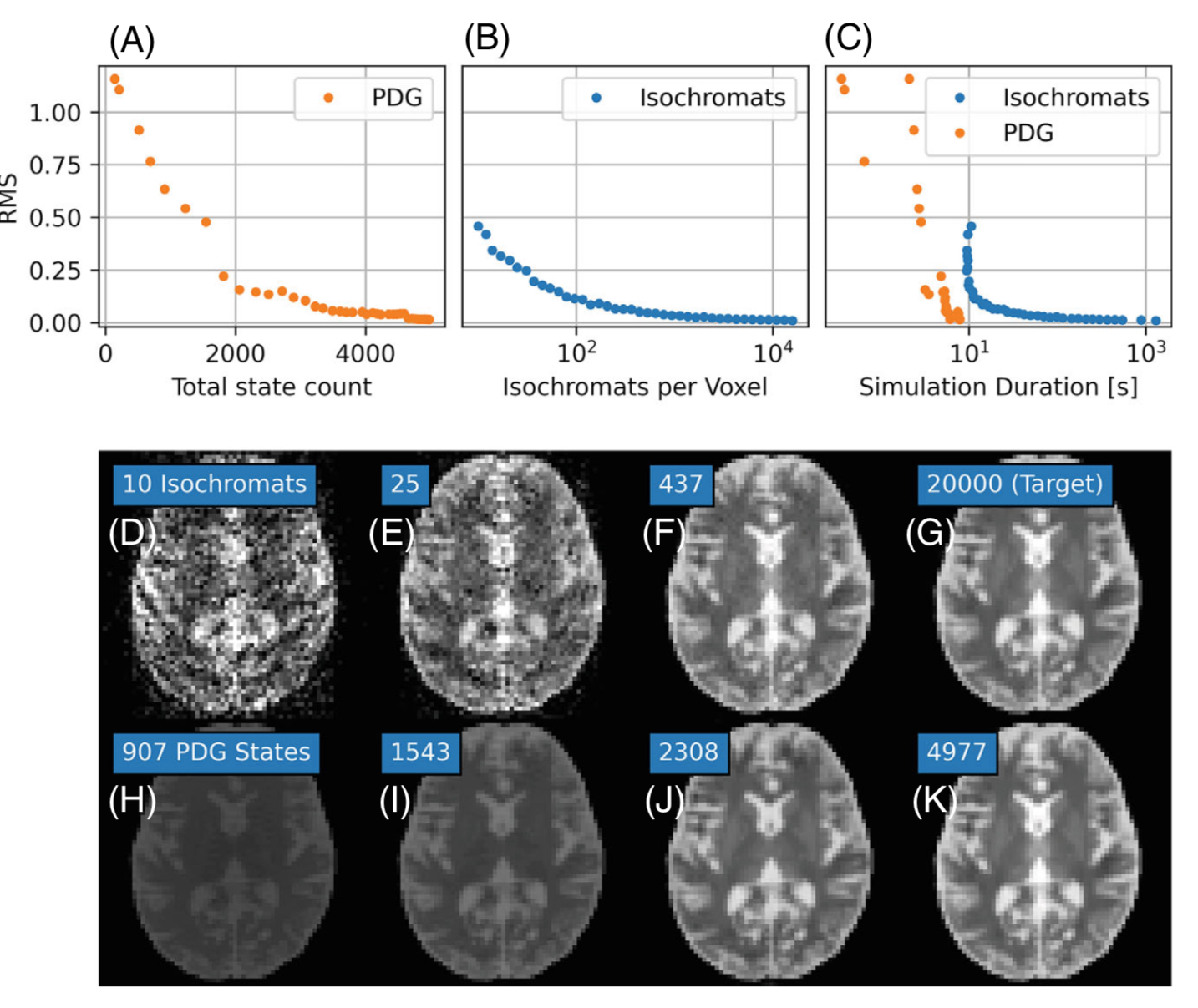

Figure 3 shows the phase graph plot of the emitted signal and the newly introduced latent signal. The latter is used to select the important states of the sequence. Stronger relaxation or diffusion actually reduces the number of necessary states for a given accuracy.

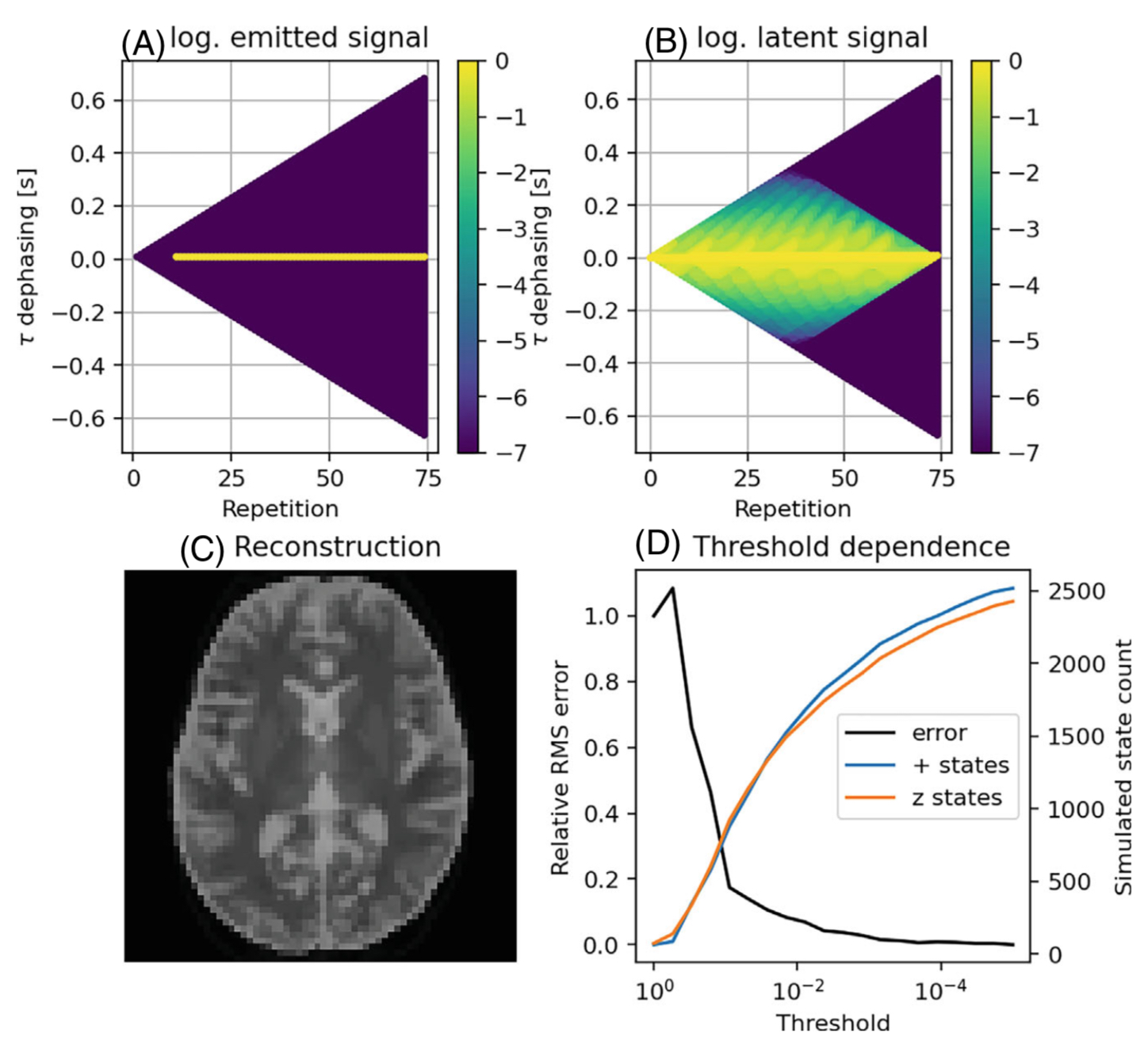
With this approach we optimized several MRI sequences (data not shown) with regard to artifacts (FLASH), blurring (TSE) and homogeneity (pTx-TSE).

Discussion and Conclusion

In this work, we derived and implemented a fully differentiable Bloch simulation based on the principles of EPG. Contrary to current EPG simulations, it is capable of simulating the actual MRI signal of arbitrary sequences, while exhibiting the same advantages like efficient computation and no simulation noise. This makes it possible to simulate and optimize sequences that otherwise would need a vast number of isochromats to be described correctly, making it a suitable replacement for these applications. Furthermore, additional analysis of magnetization and signal is possible that is not available with other simulation techniques.
The differentiable implementation allows gradient descent optimization of all parameters.

Open Science

All codes are documented and available open source via
https://mrzero-core.readthedocs.io/

Speaker: Prof. Moritz Zaiss (FAU)

12:00 PM Motion-compensated cardiac MRI reconstruction with stochastic optimisation

A 3D whole-heart MR acquisition with high spatial resolution can take several minutes. During this time, the heart is constantly moving due to breathing and the heartbeat, which can cause severe motion artefacts in the final image. To minimize these artefacts, motion correction approaches have been proposed. In this work, we utilise a motion-corrected image reconstruction (MCIR) approach. For this the acquired data is first split into n parts, corresponding to n motion states. Image registration is then used to determine the spatial transformation of each state with respect to a reference motion state. The obtained motion vector fields are subsequently used during image reconstruction to obtain a single motion-corrected MR image. While this approach leads to good image quality, the reconstruction times scale with the number of motion states. Especially for cardiac MRI, where both cardiac and respiratory motion need to be corrected, a high number of motion states might be necessary for an accurate result. Moreover, to achieve high image quality, iterative optimisation algorithms involving regularisation are used, which increases the reconstruction time. In this presentation, we demonstrate a stochastic optimisation approach which requires very few epochs and hence shorter reconstruction times compared to commonly used optimisation schemes. We evaluate the improved convergence in phantom experiments with simulated motion and demonstrate it on a cardiac 3D whole-heart scan obtained in-vivo.

Speaker: Letizia Protopapa (Science and Technology Facilities Council, UK)

11:00 AM → 12:30 PM MS 09: Stochastic Modeling and Control: MS09-4

11:00 AM Systems of quadratic growth backward SDEs in general filtration with no driving martingale

Let $(\Omega,\mathcal F,P)$ be a complete probability space and $\mathbb F:=(\mathcal F_t)$ be a filtration on $(\Omega,\mathcal F,P)$ satisfying usual conditions. Let $T>0$, $\nu$ be a natural number, and $\xi$ be an $\mathbb R^\nu$-valued $\mathcal F_T$-adapted random vector. We shall present the existence results for the following system of quadratic growth (with respect to $M$) backward SDEs of the form
\begin{equation}
Y^j_t=\xi^j+\int_t^TdF^j(s,Y,M)-\int_t^TdM^j_s,\quad j=1,\dots,\nu,
\end{equation}
where for any pair $(Y,M)\in \mathcal S^2_{\mathbb F}(0,T)\times \mathcal M^2_0(0,T)$ the mapping
\begin{equation}
[0,T]\ni s\longmapsto F^j(s,Y,M) \in \mathbb R
\end{equation}
is a finite variation continuous $\mathbb F$-adapted process with $F(0,Y,M)=0$. Then some application will be presented.

Speaker: Tomasz Klimsiak (Nicolaus Copernicus University in Toruń)

11:30 AM Optimal Estimation of Generic Dynamics by Path-Dependent Neural Jump ODEs

In this talk we study the problem of (online) forecasting general stochastic processes using a path-dependent (PD) extension of the Neural Jump ODE (NJ-ODE) framework. While NJ-ODE was the first framework to establish convergence guarantees for the prediction of irregularly observed time series, these results were limited to data stemming from It\^o-diffusions with complete observations, in particular Markov processes, where all coordinates are observed simultaneously. In this work, we generalise these results to generic, possibly non-Markovian or discontinuous, stochastic processes with incomplete observations, by utilising the reconstruction properties of the signature transform. These theoretical results are supported by empirical studies and synthetic and real world datasets. This is joint work with Marc Nübel and Josef Teichmann.

Speaker: Florian Krach (ETH Zürich)

12:00 PM Improving accuracy of ODE solvers via randomization

Randomization improves the rate of convergence of numerical schemes for ordinary differential equations. In this talk, we will present error bounds and discuss optimality (in the Information-Based Complexity sense) for selected randomized ODE solvers. Error analysis will be performed assuming low regularity of the right-hand side function (local Holder and Lipschitz continuity in time and space variables, respectively). Moreover, we will investigate the case of inexact information. Finally, we will show results of numerical experiments confirming the theoretical findings.

Speaker: Tomasz Bochacik (AGH University of Krakow)

12:30 PM → 2:00 PM Lunch

2:00 PM → 3:00 PM Contributed Talks: CT2

2:00 PM Mixed-integer linear programming models for Autonomous Home Energy Management Systems

The integrated optimization of all energy resources (exchanges with the grid, loads, storage, microgeneration) requires Autonomous Home Energy Management Systems (AHEMS) located behind the meter, which are equipped with optimization models and algorithms capable of making decisions according to the consumer’s preferences concerning the economic and comfort dimensions. For this purpose, it is necessary to develop optimization models respecting the physical operation and control principles of the appliances as well as their habitual utilization patterns and control modes. A balance should be sought between the model detail level and the computational requirements to obtain practical solutions, having in mind their implementation in AHEMS running on low-cost processors. According to the type of control, residential loads can be categorized as: shiftable (the operation cycle cannot be interrupted), interruptible (the operation can be interrupted and resume operation at a later stage), and thermostatic (the operation is controlled by a state variable such as indoor temperature).
A comprehensive set of mixed-inetger linear programming (MILP) models of appliance operation is presented, which are aimed at being seamlessly incorporated in AHEMS allowing for the integrated optimization of all energy resources. These models take into account several parameters as operation cycles requiring different power at different stages, the behavior of a thermostat with hysteresis, main principles of heat transfer in buildings. Different cost objective function components (energy and power costs, and monetized discomfort) are presented, as well as ways of dealing with the possible user’s discomfort derived from operating appliances out of the habitual periods/settings and/or temperature ranges. The computational efficiency in real settings considering a fine-grain time discretization is discusserd. These modular models are developed in a building block manner enhancing the flexibility of their utilization in overall models with different objectives encompassing the economic and comfort dimensions.

Speaker: Prof. Carlos Henggeler Antunes (Department of Electrical and Computer Engineering, University of Coimbra)

2:20 PM Power Swaps: A Coordination Mechanism for Operation of Jointly Owned Hydropower Reservoirs

In the era of energy transition, the quest of sustainability has accelerated the integration of renewable sources, highlighting the critical role of energy storage in enhancing the system’s flexibility. Within this circumstances, shared energy storage emerges as a crucial concept necessitating coordination for optimized operation of its different owners. Typical hydropower systems comprise several power plants often subject to joint ownership of shared energy storage. To efficiently deal with the challenge of handling different supply purposes in up and downstream reservoirs, a coordination mechanism is needed. This study analyzes an interesting coordination mechanism where virtual individual reservoir levels and power swaps are elements that contributes to ensuring fair utilization of the shared resources whilst respecting the concern of operating independently. Through developing a new stochastic programming model for bid optimization, we explore the economic impacts of our approach. Our findings highlight the mechanism's robustness to different operational strategies of stakeholders, its capacity to generate stable outcomes, and the economic feasibility. We contribute to the literature of sustainable management of shared hydropower resources which can be applied in other cases.

Speaker: Hossein Babazadeh (NTNU)

2:40 PM Vitali variation error bounds for expected value functions

In this paper we derive error bounds for one and two-dimensional expected value functions that depend on the Vitali variation of the joint probability density function of the corresponding random vector. Contrary to bounds from the literature, our bounds are not restricted to underlying functions that are one-dimensional and periodic. Moreover, we show that our new bounds are tighter when the components of the random vector are independent and have marginal densities with total variation less than one. In our proof, we first derive the bounds in a discrete setting, where we show that the extreme points in this setting are the set of all matrices that have zero-sum rows and columns and have an $L_1$-norm bounded by one. This result may be of independent interest. Finally, we numerically illustrate the performance of our new bounds by applying them to convex approximations of stochastic integer programs from the literature.

Speaker: Alban Kryeziu (PhD candidate)

2:00 PM → 3:30 PM MS 07: Modeling, Analysis and Optimal Control of Infinite Dimensional Problems and Applications: MS 07-1

2:00 PM On solutions to the reduced plate model with hinged-free boundary conditions

In this presentation we investigate the solutions to the reduced plate model, with hinged-free boundary conditions and action of wind in the chord-wise direction, given as:
$$\begin{array}{rcl} u_{tt}+ku_t+\Delta^2 u+[P-S\int_{\Omega}u_x^2]u_{xx}=g+\alpha u_y & \text{in} & \Omega\times(0,T)\\ u=u_{xx}=0 & \text{on} & \Gamma_D\\ u_{yy}+\sigma u_{xx}=0,\quad u_{yyy}+(2-\sigma)u_{xxy}=0 & \text{on} & \Gamma_N\\ u(x,y,0)=u_0(x,y),\quad u_t(x,y,0)=v_0(x,y) & \text{in} & \Omega. \end{array}$$ Here $\Omega\in \mathbb{R}^2$ is closed rectangle domain, $P>0$ is prestressing force and $S\geq 0$ is a coefficient to the restoring force resulting from the nonlocal stretching effect in the $x$-direction. In this reduced model, the plate possesses external forces $g$ acting in a normal direction to the plate, which represents the time-delay forces. We study the solutions of the linearized case by comparing the dependence upon the factor of the difference of prestressing and restoring forces $\mu\in \mathbb{R}$, and a factor of the strength of the wind $\alpha\in \mathbb{R}$. The numerical results will be given by using different discretization methods. The dependence of considered coefficients upon the eigenvalues for the linearized PDE will be studied.

The talk present the results of an ongoing work with prof. Irena Lasiecka, dr Raj Dhara and dr Katarzyna Szulc.

Speaker: Krzysztof Rutkowski (Systems Research Institute Polish Academy of Sciences)

2:30 PM Stabilization of a weak viscoelastic wave equation with variable coefficients and an interior delay under nonlinear boundary dissipation

In this paper, we investigate the stabilization of a weak viscoelastic wave equation with variable coefficients and an interior delay, which is also subject to a nonlinear boundary dissipation. The existence of weak solution is demonstrated by means of nonlinear semigroup theory. It is noteworthy that the system is non-dissipative. The exponential decay for energy, contingent upon the behavior of viscoelastic effects and strength of delay is achieved subject to sufficiently strong mechanical boundary damping. The precise ranges of admissible parameters ensuring the stability are provided. The methods of proofs are routed in Riemanian geometry.

Speaker: Shengjie Li

3:00 PM The Westervelt-Rayleigh-Plesset model of ultrasound contrast imaging with microbubbles

In ultrasound imaging, microbubbles are increasingly being used to improve image resolution. Ultrasound propagation through a bubbly liquid can be modeled using a nonlinear acoustic wave equation for the acoustic pressure coupled to a singular second-order ordinary differential equation for bubble dynamics. Additionally, the wave equation may involve time-fractional dissipation to capture the attenuation of acoustic waves in tissue media. In this talk, we will discuss these modeling aspects and then focus on the well-posedness analysis of a possible resulting system consisting of the (non)local Westervelt equation and the Rayleigh-Plesset equation. Numerical experiments will illustrate the single bubble dynamics and the interaction of the microbubbles and ultrasound waves. The talk is based on joint work with Teresa Rauscher (University of Klagenfurt, Austria).

Speaker: Vanja Nikolic (Radboud University)

2:00 PM → 3:30 PM MS 12: Innovative Methods for Shape Optimization: MS 12-1

2:00 PM A combined phase field and sharp method for shape optimisation

In this talk, we will consider a novel strategy for the approximation of optimal shapes. The approach is to use a phase field to provide a near-optimal shape. When adaptively refining the phase field, one ensure a well resolved interface. Upon meeting a desired stopping criteria, the level set of the phase field, which defines a shape is passed onto a sharp interface shape optimisation method. A discussion of the numerical treatment as well as some experiment will be provided.

Speaker: Philip Herbert (University of Sussex)

2:30 PM Polytopic dG-based level-set shape optimization

The well-established level-set shape optimisation method is based on the implicit description of domain boundaries as zero-level sets of a level-set function. Within this framework, domains are updated by evolving the level-set function according to a Hamilton-Jacobi equation, which itself comprises shape gradients as velocity terms.

The common approach is to employ standard finite elements to compute shape gradients and either finite elements of finite differences to solve the relevant Hamilton-Jacobi equation. In this talk, we present a different approach based on polytopic discontinuous Galerkin methods and explore its potential in terms of stability and accuracy.

Speaker: Alberto Paganini (University of Leicester)

3:00 PM Limiting Descent Directions in p-Harmonic Shape Optimization

Shape optimization constrained to partial differential equations is a vibrant field of research with high relevance for industrial-grade applications. Recent developments suggest that using a $p$-harmonic approach to determine descent directions is superior to classical Hilbert space methods. This applies in particular to the representation of kinks and corners in occurring shapes. However, the approach requires the solution of a vector-valued $p$-Laplace problem with a boundary force for each descent direction. We present an algorithm to solve these problems for finite $p$ efficiently and discuss extensions to the limit setting. A key challenge in this regard is that the Lipschitz deformations obtained as solutions in limit setting are in general non-unique. Thus, we focus on solutions which are in a sense limits to solutions for finite $p$ and aim to preserve mesh quality throughout the optimization.

Speaker: Henrik Wyschka (Universität Hamburg)

3:30 PM → 4:00 PM Coffee Break

4:00 PM → 5:00 PM Plenary Talk

4:00 PM Rare and extreme events in PDE systems involving random parameters

Estimation of tail probabilities in systems that involve uncertain
parameters or white noise forcing is important when these unlikely
events have severe consequences. Examples of such events are
hurricanes, energy grid blackouts or failure of engineered
systems. After explaining the challenges of estimating rare event
probabilities, I will make a connection between extreme event
probability estimation and PDE-constrained optimization that is
made precise by large deviation theory. The approach leads to practical methods to estimate small probabilities, and a novel class of challenging, large-scale constrained optimization problems. I will
show examples governed by the shallow water and the Navier Stokes
equations.

Speaker: Prof. Georg Stadler (Courant Institute of Mathematical Sciences, New York University)

6:00 PM → 9:00 PM Conference Dinner

Conference Dinner during harbor boat trip.

Thursday, August 15

9:00 AM → 10:30 AM MS 07: Modeling, Analysis and Optimal Control of Infinite Dimensional Problems and Applications: MS 07-2

9:00 AM On existence of multipliers for constrained optimization problems with feasible sets involving PDE's

In the presentation we consider constrained optimization problems with equality constraints given by operator $F$ acting between Banach spaces and a number of inequality constraints. The regularity conditions for the this kind of problems ensuring the existence of Lagrange multipliers are expressed with the help e.g. of Robinson Kurcyusz and Zowe or other conditions like Aubin and Guignard, which are diffucult to be checked. In general, Slate-type conditions and surjectivity of the derivative of F at the solution point impliy Robinson Kurcyusz and Zowe regularity conditions. Our aim is to discuss regularity conditions related to the image of the derivative of $F$. We will introduce sufficient conditions for the non-emptiness of the set of Lagrange multipliers. To achieve this, we will employ a generalization of Lusternik's theorem.

Speaker: Krzysztof Leśniewski

9:30 AM Eigenvalue optimization with respect to shape-variation in electromagnetic cavities

In this talk, we consider a freeform optimization problem of eigenvalues in a particle accelerator cavity by means of shape-variations with respect to small deformations. As constraint we utilize the mixed variational formulation by Kikuchi of the normalized Maxwell’s time-harmonic eigenvalue problem. For the eigenvalue optimization, we apply the method of mappings. We show results of continuity and differentiablility of the eigenvalues and the associated eigenfunctions. Further, we derive an optimality system and the reduced cost functional by using the adjoint calculus. In addition, to solve the considered optimization problem, we present a damped inverse BFGS method. We conclude with a numerical example, which shows the functionality of the optimization method, and with an outlook where we explain ongoing work and further ideas to extend the usability of this mathematical approach to real-life problems.

Speaker: Christine Herter

10:00 AM Derivatives of Rate-Independent Operators

As rate-independent operators are not smooth, they do not possess classical derivatives. We present results on their generalized derivatives and link them to optimal control problems

Speaker: Martin Brokate

9:00 AM → 10:00 AM MS 09: Stochastic Modeling and Control: MS 09-5

9:00 AM Exploring the Brain's Complexity: Stochastic Models and Artificial Intelligence in Neuroinformatics

This work emphasizes the transformative potential of leveraging large-scale multimodal data archives in neuroinformatics research, particularly focusing on electrophysiology and neuroimaging datasets. By employing rigorous standardization and harmonization methodologies alongside state-of-the-art AI tools, these archives enable novel scientific discoveries across various brain disorders and diseases. Through detailed exploration of intricate neural networks, with a particular emphasis on conditions such as epilepsy, it is demonstrated how AI-driven approaches facilitate the extraction of nuanced insights from vast, heterogeneous datasets. By systematically integrating advanced mathematical frameworks and AI methodologies, multimodal data archives can be utilized to advance our understanding of brain disorders, offering unprecedented opportunities for groundbreaking discoveries with profound implications for neuroscience research and clinical intervention.

Speaker: Prof. Dominique Duncan (University of Southern California)

9:30 AM Optimal excitation of dynamical systems for parameter identification

Reliable simulation models are crucial in virtual engineering processes. Typically, the system of differential equations in these models is rather well known. However, the development of new product classes requires new parametrizations of the system. This often leads to vast experimental programs needed to acquire all necessary data to determine relevant parameters. The choice of experiments, i.e., how to excite the system best to obtain the relevant information, is non-trivial.
In this talk, we propose a method to optimize the system excitation w.r.t. the parameter sensitivity in a known differential equation system. We therefore model the parameters as probabilistic variables and make use of polynomial chaos expansion to augment the probabilistic equations into a deterministic surrogate model. The obtained surrogate model serves as a basis for optimization of the parameter sensitivities w.r.t. the input signal.
The proposed method allows for a systematic derivation of suitable excitation functions for the parameter identification of the system. We demonstrate the method in the context of vehicle models.

Speaker: Dr Nicola Henkelmann (Bosch Research)

9:00 AM → 10:30 AM MS 12: Innovative Methods for Shape Optimization: MS 12-2

9:00 AM Constrained Best Approximation of Shape Tensors and its Role for the Determination of Shape Gradients

A crucial issue in numerically solving PDE-constrained shape optimization problems is avoiding mesh degeneracy. Recently, there were two suggested approaches to tackle this problem: (i) departing from the Hilbert space towards the Lipschitz topology approximated by $W^{1,p^*}$ with $p^*>2$ and (ii) using the symmetric rather than the full gradient to define a norm.
In this talk we will discuss an approach that allows to combine both. It is based on our earlier work [2] on the $L^p$ approximation of the shape tensor of Laurain & Sturm [1]. There we have shown that $W^{1,p^*}$ shape gradients can be determined as Lagrange multipliers of this $L^p$ approximation problem. We extend this by adding a symmetry constraint to the derived $L^p$ least mean approximation problem and show that the distance measured in a suitably weighted $L^p$-norm is equal to the dual norm of the shape derivative with respect to the $L^{p^*}$-norm associated with the linear elastic strain of the deformation. The resulting $L^p$ least mean problem can be viewed as a generalization of a constrained first-order least squares formulation. In addition, as in the case without symmetry constraint, it turns out that the Lagrange multiplier associated with the divergence constraint is the direction of the steepest descent, but now with respect to the norm defined by the symmetric gradient. This provides a way to compute shape gradients in $W^{1,p^*}$ with respect to this elasticity type norm.
The discretization of the resulting least mean problem can be done by the PEERS element and its three-dimensional counterpart. We will illustrate the advantages of this approach by computational results of some common shape optimization problems.

References:
[1] A. Laurain and K. Sturm. Distributed shape derivative via averaged adjoint method and applications. ESAIM Math. Model. Numer. Anal., 50(4):1241–1267, 2016.

[2] G. Starke. Shape optimization by constrained first-order system mean approximation, 2023. arXiv:2309.13595.

Speaker: Laura Hetzel (University of Duisburg-Essen)

9:30 AM A W-1-∞-appraoch for Shape Optimization using ADMM

The talk discusses the efficiency and robustness aspects of a first-order approach based on ADMM (Alternating Direction Method of Multipliers) for approximating the direction of the steepest descent in $W^{1,\infty}$ with Lipschitz domains. The robustness of an implementation with respect to certain parameters is crucial for the technical application of shape optimization problems. For example, when considering large deformations, the quality of the computational grid may become insufficient and requires remeshing and, thus, user interaction after a certain number of shape updates. In addition, many implementations need a variety of user-defined parameters, e.g., penalty factors and step size values of an augmented Lagrange method, the maximum $p$-value using a $p$-Laplace relaxation of the steepest descent direction, or relaxation factors for fine-tuning the solution procedure. These parameters are usually problem-dependent, and choosing values requires expert knowledge and many experiments to determine; thus, reducing the number of input parameters improves the robustness and usability of the implementation. Although the challenges mentioned above occur in many disciplines, we focus on fluid dynamic applications here. The method is applied to the minimal drag problem and compared to a $p$-Harmonic approach. We present the results of different numerical experiments in two and three spatial dimensions for well-known example problems in fluid dynamics.

Speaker: Dr Peter Marvin Müller (Hamburg University of Technology)

10:00 AM Reducing overhangs in additive manufacturing with Shape and Topology optimization

One main goal of topology optimization is to find an optimal distribution of multiple materials in a design domain in such away that it can withstand internal and external loads applied on the structure. Additive manufacturing techniques like 3D-printing are able to produce complex structures and topologies. To guarantee constructability overhangs need either support structures or should be avoided in total. Using a phase field approach we include this restriction, by studying a control problem minimizing the weighted sum of the Ginzburg-Landau energy with the mean compliances of the whole structure and of each individual layer. To this end, we introduce multiple linear elasticity equations as state equations describing the displacement of the structure to the applied loads. To solve this problem numerically, the VMPT (Variable Metric Projection Type) method is presented and applied. Finally, we perform numerical experiments on multiple examples. The impact of model parameters on the shape and topology is discussed. Furthermore the enormous speed up with the VMPT method using variable metrics including second order information is presented.

Speaker: Maximilian Urmann (Universität Regensburg)

10:30 AM → 11:00 AM Coffee Break

11:00 AM → 12:30 PM MS 02: Robust Optimization of hybrid / nonsmooth systems: MS 02-1

11:00 AM A descent method for nonsmooth multiobjective optimization problems in Hilbert spaces

This talk is dedicated to a common descent method designed for nonsmooth multiobjective optimization problems (MOPs) with objective functions defined on a general Hilbert space that are locally Lipschitz continuous. The only strategy to handle nonsmooth MOPs in infinite dimensions besides the presented method relies on scalarization techniques, which are not suitable for MOPs with nonconvex objective functions or for MOPs with more than two objective functions. The class of nonsmooth MOPs on infinite dimensional Hilbert spaces is particularly important since it allows the formulation of PDE-constrained MOPs.
For the analysis of the presented method, we first introduce optimality conditions suitable for nonsmooth MOPs. We generalize the so-called Goldstein epsilon-subdifferential to the multiobjective setting in Hilbert spaces and describe its main properties.
Then, we introduce the mentioned descent method. The method uses an approximation of the epsilon-Goldstein subdifferential to compute a common descent direction that provides sufficient descent for all objective functions. In the main result, we show that, under reasonable assumptions, the method produces sequences that possess Pareto critical accumulation points.
Finally, we present the behaviour of the common descent method for a (PDE-constrained) multiobjective obstacle problem in one and two spatial dimensions. We show that the method is capable of producing several different optimal solutions and discuss the behaviour of the approximated subdifferential.

Speaker: Mr Konstantin Sonntag (Universität Paderborn)

11:30 AM Approximate propagation of normal distributions for stochastic optimal control of nonsmooth systems

We present a method for the approximate propagation of mean and covariance of a probability distribution through ordinary differential equations (ODE) with discontinuous right-hand side. For piecewise affine systems, a normalization of the propagated probability distribution at every time step allows us to analytically compute the expectation integrals of the mean and covariance dynamics while explicitly taking into account the discontinuity. This leads to a natural smoothing of the discontinuity such that for relevant levels of uncertainty the resulting ODE can be integrated directly with standard schemes and it is neither necessary to prespecify the switching sequence nor to use a switch detection method. We then show how this result can be employed in the more general case of piecewise smooth functions based on a structure preserving linearization scheme. The resulting dynamics can be straightforwardly used within standard formulations of stochastic optimal control problems with chance constraints.

Speaker: Florian Messerer (University of Freiburg, Germany)

12:00 PM Probability-Based Collision Risk Evaluation of Trajectories for Optimal Control Problems with Moving Obstacles

We utilize the probability distributions of the future location of moving obstacles to aid in the maneuver planning of autonomous vehicles. The result is an objective function and necessary derivatives to solve optimal control problems in a multi-shooting scheme with shooting nodes on an equidistant time grid. We evaluate the proposed objective function in different scenarios featuring obstacles governed by a single-track kinematic model. The probability distributions of an obstacle's future location are given for each time step by a probability mass function on a location grid. From these likelihoods, we derive a risk map that allows a convenient treatment of multiple obstacles and serves as the basis of the objective function.

Speaker: Prof. Matthias Gerdts (Universität der Bundeswehr München)

11:00 AM → 12:30 PM MS 07: Modeling, Analysis and Optimal Control of Infinite Dimensional Problems and Applications: MS07-3

11:00 AM Optimal Switching Dirac Control for Stabilization of Time-Varying Linear Parabolic Equations

This talk deals with infinite horizon optimal control problems governed by time-varying linear parabolic equations. We focus on controls represented by linear combinations of finitely many Dirac measures in the spatial domain, where only one measure is active at any time. This feature endows the problem with switching properties and thus transforms it into an infinite horizon nonsmooth nonconvex problem. To address this problem, we employ a receding horizon control (RHC) approach. This involves approximating the infinite-horizon problem with a sequence of finite-horizon ones over overlapping time intervals. We discuss the stabilizability and suboptimality of RHC and introduce a nonmonotone proximal gradient method to solve the nonsmooth nonconvex subproblem. We also present numerical experiments to validate the effectiveness of our approach in dealing with the complexity of infinite horizon optimal control with time-varying dynamics and switching properties.

Speaker: Behzad Azmi

11:30 AM Directional differentiability for solution operators of vectorial sweeping processes with applications in optimal control

We study directional differentiability properties of solution operators of rate-independent evolution variational inequalities with full-dimensional convex polyhedral admissible sets. It is shown that, if the space of continuous functions of bounded variation is used as the domain of definition, then the most prototypical examples of such solution operators - the vector play and stop - are Hadamard directionally differentiable in a pointwise manner if and only if the admissible set is non-obtuse. We further prove that, in those cases where they exist, the directional derivatives of the vector play and stop are uniquely characterized by a system of projection identities and variational inequalities and that directional differentiability cannot be expected in the obtuse case even if the solution operator is restricted to the space of Lipschitz continuous functions. Our results can be used, for example, to formulate Bouligand stationarity conditions for optimal control problems involving sweeping processes.

Speaker: Constantin Christof (TUM)

12:00 PM Algorithm Switching for Multiobjective Energy Modeling and Predictions

This talk explores the application of multi-objective optimization in the field of renewable energy, focusing on both classification and regression tasks driven by machine learning. We consider multiple objectives, including accuracy, computational efficiency, algorithmic bias, and model sparsity. Models can be comprehensive, ranging from complex decision trees and neural networks to simple KNN-type settings. Multi-objective derivative-free optimization has utilized Bayesian and direct-search methods individually in the past. In this work, we introduce a novel switching framework that integrates both methods iteratively. Additionally, we propose a warm-start training methodology tailored for machine learning problems, which effectively deploys the problem structure. We evaluate our proposed method by comparing it against traditional Bayesian and Direct-Search approaches using multiple real-world datasets and machine learning models. We observe a significant improvement in numerical performance with the joint switching-based scheme.

Speaker: Zijun Li (HU Berlin)

11:00 AM → 12:30 PM MS 12: Innovative Methods for Shape Optimization: MS 12-3

11:00 AM Computing Multiple Local Minimizers of Topology Optimization Problems and Application for Hydrogen Electrolysis Cell Design

Topology Optimization considers the optimization of a domain by changing its geometric properties by either adding or removing material. Typically, topology optimization problems feature multiple local minimizers. In order to guarantee convergence to local minimizers that perform best globally, it is important to identify multiple local minimizers of topology optimization problems. Moreover, finding local solutions that are desirable from an application standpoint due to easy manufacturability or aesthetic designs also requires the discovery of multiple local minimizers.

In this talk, we present a novel deflation approach to systematically find local minimizers of general topology optimization problems. The approach is based on a penalization of previously found local solutions in the objective. Through a series of examples, including the optimization of fluids in Stokes flow and the optimization of bipolar plates in hydrogen electrolysis cells, we demonstrate the effectiveness of our approach.

Speaker: Leon Baeck (Fraunhofer Institute for Industrial Mathematics ITWM)

11:30 AM Continuation methods for higher-order density-based topology optimization

We aim to solve a topology optimization problem where the distribution of material in the design domain is represented by a density function. To obtain candidates for local minima, we want to solve the first order optimality system via Newton's method. This requires the initial guess to be sufficiently close to the a priori unknown solution. Introducing a stepsize rule often allows for less restrictions on the initial guess while still preserving convergence. In topology optimization one typically encounters nonconvex problems where this approach might fail. We therefore opt for a homotopy (continuation) approach which was first introduced in the 1980s and is based on solving a sequence of parameterized problems to approach the solution of the original problem. The arising Newton-type method also allows for employing deflation techniques for finding multiple distinct solutions as well as for efficiently tracing Pareto optimal points in multi-objective optimization problems.
We show numerical results for the design optimization of an electric machine.

Speaker: Michael Winkler (RICAM)

12:00 PM Combined topology-parameter multi-material optimization by the topological derivative

We consider a PDE-constrained design optimization problem with multiple materials, where some material properties are defined by an additional parameter. For this problem we derive the topological derivative i.e. the pointwise sensitivity of the cost functional subject to material changes and use it to update a vector-valued level set function describing the material distribution within the design domain. In an additional step we simultaneously optimize the material parameter by minimizing the topological derivative. This we can do either pointwise, resulting in a parameter distribution, or blockwise by averaging the topological derivative. The latter approach would lead to a fixed number of different parameters which could increase the manufacturability of the design. We apply this approach to two engineering problems: First a permanent magnet synchronous electric machine where we optimize not only the design but also the orientation of the permanent magnets and second a cantilever where we parametrized the lattice microstructure of the material.

Speaker: Nepomuk Krenn (Johann Radon Institute for Computational and Applied Mathematics (RICAM), Austrian Academy of Sciences)

12:30 PM → 2:00 PM Lunch

2:00 PM → 4:00 PM Plenary Talk

2:00 PM Bilinear control problems governed by PDEs: analysis, optimization and discretization

Despite its importance in applications, there are not many references dealing with the analysis of bilinear control problems governed by elliptic partial differential equations.

In this talk, we will deal with an optimal control problem where the control acts in a multiplicative way. We will investigate both the case in which the control is the reaction coefficient (distributed) and the case in which the control acts as the Robin coefficient on the boundary.

First we will perform a careful study of the control-to-state mapping. Differentiability in L^s for some appropriate s>=2 is not immediate. We are able to prove it and this allows us to obtain first order necessary optimality conditions and no-gap second order sufficient optimality conditions for the control problem.

Next we rewrite the problem using a semismooth equation and prove superlinear convergence of the semismooth Newton method in an infinite-dimensional framework. This is done under the assumptions of no-gap second order sufficient optimality conditions and strict non-complementarity, as is usual for this kind of algorithms in the finite-dimensional setting. Previous results in the literature assumed local convexity, which is a rather stringent assumption for bilinear control problems. An algorithm is provided. The 3D boundary problem represents a challenge due to the lack of differentiability in L^2.

Finally, we discretize the problem using finite elements. We will show results for the distributed case. Piecewise constant functions are used to approximate the controls, while continuous piecewise linear functions are chosen to approximate both the state and the adjoint state variables. Convergence and error estimates are obtained assuming no-gap second order sufficient optimality conditions. For the control, the obtained order of convergence is O(h), while for the state and adjoint state we are able to prove order O(h^2). This kind of behaviour where the order of convergence found in numerical experiments for the state is better than the one expected from the error in the control is very usual in control problems. It is normally referred to as superconvergence.

Numerical experiments that confirm all our findings will be presented.

This conference gathers results obtained in collaboration with Eduardo Casas and Konstantinos Chrysafinos.

Speaker: Prof. Mariano Mateos (Universidad de Oviedo)

3:00 PM Opinion formation and control

There is a large literature on opinion formation models; in many of them the dynamics are driven by binary interactions between individuals that are modulated by an underlying (social) network structure. In this talk I will discuss different mathematical modeling approaches in this setting, and how we can derive partial differential equation models in suitable scaling limits. Furthermore I will focus on the question of opinion control; in particular the question of how one can steer an opinion towards a desired target or prevent consensus.

Speaker: Prof. Marie-Therese Wolfram (University of Warwick)

4:00 PM → 4:30 PM Coffee Break

Friday, August 16

9:00 AM → 10:30 AM MS 02: Robust Optimization of hybrid / nonsmooth systems: MS 02-2

9:00 AM Accelerating a Bike Without Pedaling – A Benchmark Problem for Nonsmooth Optimal Control?

In this talk, we propose a benchmark problem for numerical nonsmooth optimal control, tailored for systems with autonomous state jumps. In particular, these challenges are posed by mechanical systems with inherent nonsmoothness, characterized by abrupt jumps in both states and dynamics. Our proposed benchmark scenario involves accelerating a bicycle along an uneven mountain bike track without pedaling—a quintessential maneuver in pump track biking, a discipline where momentum is generated through upper body movements.

This application underscores the practical relevance of nonsmooth methods for calculating optimal riding strategies in a real-world setting. This stands in contrast to conventional academic examples such as bouncing balls, which often feature purely abstract control inputs. We present numerical and experimental results.

Speaker: Julian Golembiewski (Institute of Energy Systems, Energy Efficiency and Energy Economics, TU Dortmund University)

9:30 AM IFDIFF - A Matlab Toolkit for ODEs with State˗Dependent Switches

Several formulations for robustified optimization problems incorporate first-order derivatives of the original objective. In dynamic optimization settings, this usually involves the computation of sensitivities w.r.t. initial values and parameters of the underlying differential model.
We present the toolkit IFDIFF [1] for integration and sensitivity generation in parameterized implicitly (state-dependent) switched ODEs whose right-hand side is given as Matlab code containing non-differentiable operators (max, abs, etc.) and conditionals (if).
Naive implementations using IF-THEN-ELSE branching give unreliable simulation results without warning, as switching events are undetectable by standard integrators. The widespread belief that this can be countered using more stringent integration tolerances is wrong: We give a simple example where the integrator’s error estimation always delivers zero.
Correct treatment of switched systems requires elaborate formulation of switching functions and tailored integrators, placing high mathematical demands on modelers. Even small model changes often imply considerable reformulation effort. Further, n switches generate up to $2^n$ possible program flows and switching functions, rendering a-priori formulations infeasible already in medium-sized models.
IFDIFF programmatically handles switching events, auto-generating only required switching functions. It determines switching times up to machine precision, and ensures accurate simulation and sensitivity results. Transparently extending the Matlab integrators (ode45, ode15s, etc.), IFDIFF is applicable to existing code with state- and parameter-dependent conditionals, thus enabling fast prototyping and relieving modelers of mathematical-technical effort.

[1] IFDIFF - A Matlab Toolkit for ODEs with State˗Dependent Switches, https://andreassommer.github.io/ifdiff/

Speaker: Andreas Sommer (IWR - Uni Heidelberg)

10:00 AM Towards robust optimization of chromatographic separation processes with flow reversal

Column liquid chromatography plays an important role in the downstream processing of biopharmaceuticals, where the goal is to capture and purify a target protein from a mixture. Our goal is to employ a model-based approach for process optimization to improve the quality of the product, while also achieving further economical and ecological benefits.

Rate models in combination with suitable reaction schemes that model the specific adsorption process are often employed to describe chromatographic processes. The optimal control problems (OCPs) are hence governed by advection-diffusion-reaction-type partial differential equations (PDEs) with high nonlinearities. Furthermore, at least one flow reversal is typically performed in practical applications to obtain sharper elution profiles, thus leading to switching dynamics. Lastly, it is important to determine robust solutions in order to safeguard against, e.g., uncertain model parameters, such as reaction rates and feed composition.

In this talk we present developments towards robustly optimal switching control applied to chromatographic separation processes and discuss the obtained results.

Speaker: Dominik H. Cebulla (Institute for Mathematical Optimization, Technische Universität Braunschweig)

9:00 AM → 10:30 AM MS 07: Modeling, Analysis and Optimal Control of Infinite Dimensional Problems and Applications: MS07-4

9:00 AM Solving Discrete Quantum Optimal Control Problems

We present a family of discrete optimal control problems that are motivated by quantum pulse optimization to design quantum gates. We solve the continuous relaxation using the gradient ascent pulse engineering (GRAPE) algorithm, and apply combinatorial integral approximation (CIA) techniques to obtain discrete optimal controls. To add constraints and more complex regularization terms, we develop an alternating direction of multiplier (ADMM) method. We show empirically that ADMM improves the rounding results of CIA compared to GRAPE. Time permitting, we also comment on methods and models that can optimize under uncertainty, and show recent results that indicate that taking uncertainty into account can be critical for optimal control.

Joint work with: Xinju Fei (University of Michigan), Siqian Chen
(University of Michigan), Jeff Larson (Argonne National Laboratory).

Speaker: Prof. Sven Leyffer (Argonne National Laboratory)

9:30 AM A variational and numerical approach to model inverse problems applied in subduction earthquakes

This talk presents a mixed variational formulation for the problem of the elasticity equation with jump conditions in an interface with the purpose of modeling subduction earthquakes by introducing the concept of coseismic jump. For this new problem, we introduced an optimal control problem that seeks to recover the coseismic jump from boundary observations. Both problems can be discretized by applying mixed finite elements. Synthetic results applied to a realistic context will be presented.
Finally, we analyze some improvements for the numerical discretization and preliminary ideas of an inverse inequality that ensures the uniqueness and stability of the solution of the inverse problem.

Speaker: Dr Jorge Aguayo Araneda (Centro de Modelamiento Matemático - Universidad de Chile)

10:00 AM Combined Regularization and Discretization of Equilibrium Problems and Primal-Dual Gap Estimators

The present work aims at the application of finite element discretizations to a class of equilibrium problems involving moving constraints. Therefore, a Moreau–Yosida based regularization technique, controlled by a parameter, is discussed. Using an extended $\Gamma$-convergence, a priori convergence is derived. This technique is applied to the discretization of the regularized problems. The convergence of the surrogate problems is shown, when regularization and discretization are applied simultaneously. A primal-dual gap technique is used for the derivation of error estimators suitable for adaptive mesh refinement. In addition, a strategy for balancing between a refinement of the mesh and an update of the regularization parameter is established. The theoretical findings are illustrated for the obstacle problem. Numerical experiments are performed for two quasi-variational inequalities with application to thermoforming and biomedicine, respectively.

Speaker: Steven-Marian Stengl (Technische Universität Berlin)

9:20 AM → 10:00 AM Contributed Talks: CT3

9:20 AM Rate of Penetration Optimization using Differential Evolutionary Extreme Learning Machines

This paper is an extension of a prior work on the optimization of the rate of penetration (ROP) using Differential Evolutionary Extreme Learning Machines (DEELM). ROP is a major concern in oil drilling industry. The optimization procedure aims eventually to identify drilling parameters resulting in a maximum ROP and minimum drilling cost. In this work we propose the usage of a variant of extreme learning machine (ELM) that parameters are optimized through a differential evolution inner loop. This forms the DEELM. The ROP results are compared with a multiple nonlinear regression model and feed forward neural networks in terms of accuracy and time complexity. The data for drilling parameters will be inputted and rate of penetration (ROP) will be the output. After model building training and optimizing, recommendations about the optimum drilling parameters will be provided to the users.

Speaker: Amar Khoukhi (York College, CUNY)

9:40 AM Multilinear Hybrid Differential Algebraic Models - Challenges & Applications

Many engineering applications deal with systems which can be modeled adequately by nonlinear DAEs with mixed-integer variable spaces. For this generic case, no structured representation - like the parameter matrices for continuous-variable linear DAEs - are possible. This changes, if the occuring functions are restricted to be multilinear, where the parameters can be represented as tensors. That opens the door to efficient simulation, analysis, and model reduction methods by tensor decomposition algorithms. Multilinear Hybrid Differential Algebraic Models and efficient computation methods will be introduced in the presentation. Their usefulness for control and diagnosis problems will be discussed for HVAC systems as well as power networks.

Speaker: Gerwald Lichtenberg (HAW Hamburg)

10:30 AM → 11:00 AM Coffee Break

11:00 AM → 12:00 PM Plenary Talk

11:00 AM Discrete-To-Continuum Limits in Graph-Based Semi-Supervised Learning

Semi-supervised learning (SSL) is the problem of finding missing labels from a partially labelled data set. The heuristic one uses is that “similar feature vectors should have similar labels”. The notion of similarity between feature vectors explored in this talk comes from a graph-based geometry where an edge is placed between feature vectors that are closer than some connectivity radius. A natural variational solution to the SSL is to minimise a Dirichlet energy built from the graph topology. And a natural question is to ask what happens as the number of feature vectors goes to infinity? In this talk I will give results on the asymptotics of graph-based SSL. The results will include a lower bound on the number of labels needed for consistency and insights from the analysis will lead to a new SSL algorithm for the low-label regime. Furthermore, the approach inspires a modification of diffusion based graph neural networks.

Speaker: Prof. Matthew Thorpe (University of Warwick)

12:00 PM → 12:30 PM Opening/Closing: Closing

12:30 PM → 1:30 PM Lunch